抛物线和椭圆的经典例题（用无穷大的思想分析椭圆）

本篇用无穷大的思想将一个一般方程变成椭圆，双曲线，抛物线方程。即简单又容易理解。

我们知道二次曲线的通用方程：

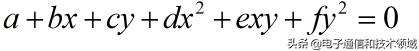
经过改写：

所以每个横坐标X有两个纵坐标与之对应，或者没有纵坐标与之对应，因为y的根为实数或者为虚数。而椭圆，抛物线，双曲线正是从这个方程中分离出来，变成独立的曲线。

当坐标系原点在图形中心点时，y的两个值肯定大小相等，符号相反，所以和为0，所以

此时二次曲线通用方程的形状为：

此处 b d取不同的值时，将会产生不同的圆锥曲线。

第一双曲线：当d>0，x趋于正无穷大时:

因此表达式（1）为正，纵坐标y有两个无穷大的值，一正一负，

当x趋于负无穷大时，表达式（1）仍为正，纵坐标y有两个无穷大的值，一正一负，

所以d>0时，二次曲线有四条伸向无穷远的分支，x趋于正无穷大时两条，x趋于负无穷大时两条。这就是双曲线的来源。

双曲线方程：

第二椭圆：当d<0时，x趋于正无穷大和负无穷大时，表达式

所以纵坐标y都是虚数（或不存在）,可见d<0时，曲线的纵坐标都不能为无穷大，即曲线没有伸向无穷的分支，整个曲线位于一个确定的有限范围之内，这样的二次曲线就是椭圆。

椭圆方程：

所以d>0或d<0二次曲线截然不同，决定了两种曲线，

第三抛物线：当d=0时，因为0在正负之间，所以这时的曲线性质也在双曲线和椭圆之间。

此时方程变为

b为正为负都可以，当b>0时，X趋于正无穷时，y也趋于无穷大,且一正一负。

当b>0时，X趋于负无穷时，y为虚数（不存在）

所以当d=0，b>0时，二次曲线有趋于无穷的两个分支。且只有两个分支，这就是抛物线。

抛物线方程：

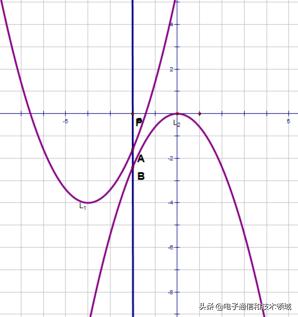
上述就是用无穷大思想分析一般通用方程得到三种不同的曲线。