梯度下降和最小二乘（梯度下降和二阶导数的最优学习率）

在几何上，函数的梯度是什么?

为什么我们需要知道这些?

坡度下降的简要概述:如果你在山坡上，你想尽快到达谷底，你不遵循等高线，这会保持你的高度不变。迭代的过程是去到下一个较低的等高线，取最短和最陡的步骤，或者相等地，走到尽可能低的等高线，保持你的步长不变。现在你可以把轮廓想象成(局部)平行的曲线集合，见下图。但是一步是一个方向和长度。直观上，我们想要“垂直”的步骤到轮廓:到最近的点在较低的轮廓。我们如何展示这个，如何从一组几乎平行的曲线中“数学地”得出函数的方向?

在很多关于机器学习的介绍性讲座中，为了使一个变量的函数极端化，建议将学习率设置为二阶导数的倒数。将其推广到多个维度涉及“... Hessian ...”。

如果你对微分学很熟悉，你可以直接跳到最后。一般论点如下:

• 在函数f的任何谷值中，你要最小化，将函数展开成(多维)泰勒级数关于任意初始点x0。
• 通过在位移（x x0）中只保留两个项的条件来近似这个函数。
• 通过把它的导数设为0来求极值。
• 求出从x到最小二次逼近f的位移。
• 这就产生了理想的步骤是Hessian乘以(负的)梯度的逆。

为了了解二阶导数和Hessians，理解以下内容对我很有帮助。

（real）函数是空间到实数的映射。如果它是二维的函数，那么在二维的任意点(x,y)函数会给你一个实数。这可以通过多种方式实现:

• 作为一组值(x,y, f(x,y))，
• 一种数值计算方法
• 在所谓的“封闭”函数形式中，例如f(x, y) = y*sin(3*x)(作为数值计算的简写)。

函数是什么样子的?你可以在三维空间中把它表示为z = f(x,y)的曲面，或者在二维空间中表示为地形图:

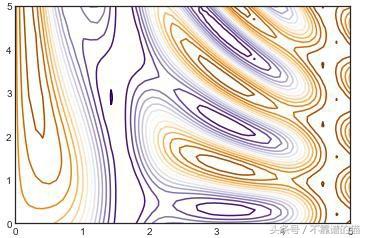
用2D表示一个函数

它的梯度是什么？函数的梯度是等高线图！在这种情况下，它不是一个常数，就像流体流动可能在不同点上指向不同方向的矢量一样。但梯度不是矢量，它是一个co-vector。

那么什么是covector？给定一个函数，它的梯度可以自然地构造出来，我们刚刚做到了！co-vector是梯度的总和（但它本身可能不是梯度）。

我们知道矢量v ^ a是什么样的：它是一个有方向和大小的箭头。我们甚至知道如何添加矢量：将它们头尾连接并将第一个尾部加入最后一个头部：

矢量添加

矢量场在每个点都是箭头，如果你有flow lines，那么它就是线上每一点的切线矢量。

我们已经可视化上面的梯度场，等高线图。什么是 co-vector w _ a（在某一点上）的样子？它看起来像两个平行平面：在给定点上，该点处的切平面和下一个轮廓上的切平面。在2D中，它看起来像

为什么叫co-vector和它是什么?co-vector是一个从向量线性映射(在本例中)实数。这张地图在R中写成w _ a v ^ a = w（v）= < w，v >。我们如何计算它？它被定义为跨越矢量所需的w的数量：

Action of a co-vector on a vector

在这种情况下，w（v）= 2，因为你必须放置两个w的“head-to-toe”来跨度v。这里有两点：首先，两个w的“head-to-toe”不是2 * w，其次，w（v）取决于v和w的大小以及它们的相对方向。

加入Covector：

加入Covector

当covector变大时，线(或平面)就会越来越近!请注意，在等高线图中，这也很直观:最陡的部分是等高线之间的紧密间隔。

到目前为止，用梯度下降法最小化函数的要点如下:

• 我们想知道往哪个方向走，走多少步。这是一个位移，因此是一个带有“Upper”索引的向量，或者一个(1,0)类型的张量，或者一个列矩阵
• 我们知道函数的轮廓以及梯度
• 但梯度是一个简单的（局部）函数的下一个轮廓线的位置，因此它是一个具有“较低”索引或者类型（0,1）张量或行矩阵的co-vector。
• 如何从行矩阵到列矩阵?
• 我们需要一列或者一个类型为（2,0）的张量，即类似T ^ { ab }的东西，这样v ^ a = T ^ { ab } w _ b。
• 几何上，我们需要把轮廓线转换成箭头。
• 我们认为这是显而易见的，因为我们进入了(一个很好的近似)欧几里得空间。
• 但是在权值x的空间中，损失是我们要最小化的权值的函数，即使经过归一化，也没有自然度量。

在矩阵代数中，单位矩阵是一种类型的张量(1,1)，一列或一行。允许我们从列向量到行向量的“转置”操作隐式地假设并使用欧几里德类型(2,0)张量((1,0,0)，(0,1,0)，(0,0,1))，这是一排“行”。这不是单位矩阵，它是(1,1)张量。

让我们先求出理想的步骤，或者说，学习率，在一维情况下。

1维二次方的理想学习率

考虑一个二次方程作为要在一维空间{ x }中被最小化的损失函数（在一个特定的谷中）的近似，并且假设我们已经知道它的函数形式。

要最小化的损失或函数是（注意，我们现在使用y作为目标函数而不是变量）

y = f（x）= a * x ** 2 b * x c

其在任何点x的梯度或导数都是

d y（x）= f '（x）= 2 * a * x b

其二阶导数是

dd y = f ''（x）= 2 * a

这个函数的最小值是

X = arg（min（y））= argmin（y）

通过设置y的一阶导数找到，d y（X）= 0。

所以我们得到X = - b /（2 * a）

现在想象一下，我们已经开始在一些任意的初始点X 0，我们希望得到X。梯度下降：

• 在x 0 处评估导数：d y（x 0）
• 步骤在相反的方向，以X 1 = X 0 δ X，其中，δ X =-α* d ý（X 0）
• 但是多少？这是学习率 α

我们如何优化α，让我们以最少的步数达到最低点？你可以说，我们从x 0 开始，我们想要到达X，如果我们选择x 1 = X，我们可以一步完成

δx = x1 — x0 = X — x0 = -(x0 b/(2*a)).

问题是，当我们在某个任意点x 0 开始时，我们只有一种计算任何点的损失函数值的方法，我们不知道什么是a，b，c，甚至不是X = - b /（2 * a）。这类似于在山坡上漫步，在浓雾中，只有一个高度计，并面临到达谷底的问题。

我们所知道的是如何为任何x计算y（x）。所以我们可以计算y（x 0）。我们也可以计算它的导数。怎么样？我们可以计算y（x 0 ε）并选择ε“足够小”：

dy(x0) ~= (y(x0 ε) — y(x0))/ ε

这足以让我们弄清楚如何到达底部？不，因为如果我们只知道一阶导数，我们将损失近似为一条直线，而切线没有关于最小值位置的信息：

两个二次曲线在一点相切

蓝色和红色曲线在x = 1时具有相同的导数，但它们分别在-0.5和 0.25处具有最小值。显然，为了得到最小值，我们需要知道曲线是怎样的。

所以回到损失函数的二次近似。我们知道这一步与梯度有关：

δx = — α * dy(x0)

我们也知道梯度：

dy(x0) = f’(x) = 2*a*x0 b

我们已经想出了理想的一步

δx = x1 — x0 = X — x0 = -(x0 b/(2*a))

把它们放在一起，我们发现学习率

α = — δx/dy(x0) = 1/(2*a) = 1/ddy(x0) =二阶导数的逆。

所以理想的一步是由

δx = — dy(x0) / ddy(x0)

1维近似理想步骤

在前面的章节中，我们表明如果我们想使用“机器学习”在一维中找到二次最小值，特别是使用梯度下降，理想学习率是当前点的二阶导数的倒数。在这篇文章中，让我们尝试并将其推广到找出一维中几乎任何曲线y = y（x）的局部最小值。

在初始点x 0 附近以泰勒级数展开y（x）：

y(x) ~= y(x0) (x — x0) * dy(x0) (x — x0)**2 * ddy(x0) / 2 …

X = argmin(y(x)) 由一阶导数= 0给出:

dy(x0) (X — x0)*ddy(x0) ~= 0

=> δx = — dy(x0) / ddy(x0).

该步骤与梯度（一阶导数）的方向相反，并且学习率 - 或梯度乘以找到理想步长的因数 - 是二阶导数的倒数。

该结果与坐标无关，但非线性坐标变换将导致不同的步骤，因为y（x）中“谷”的二次近似在不同的坐标中将有所不同。

推广到多个维度

在前面的章节中，我们展示了二阶导数的倒数是对使用梯度下降找到几乎任何一维函数的最小值的理想学习率的近似值。在这篇文章中，我们将这个结果推广到多维，并展示如何通过类型（0,2）的神秘和缺失张量从梯度co-vector 到矢量步进。

我们有多个权重，我们试图使用最小化某些损失函数。所以权重空间{ x }是多维的，一个点由向量x 或x ^ a给出。损失函数y（x）可以用泰勒级数展开：

y(x) ~= y(x0) δx dy(x0) δx δx ddy(x0) / 2 …

其中dy = (∂y/∂x^i) d x^i，梯度，是co-vector，δ X 是在权重的增量变化。就组件或指数而言：

y(x) ~= y(x0) δx^i d_i y(x0) δx^i δx^j H_{ij}(x0) / 2 …

其中 H_{ij} = (∂/∂x^i) (∂/∂x^j) y

是Hessian矩阵或y的混合偏导数矩阵。

为了找到极值，我们设置= 0 梯度 y(x) w.r.t. x，并牢记 δx = x — x0:

0 = d_i y(x) = d_i y(x0) δx^j H_{ij}(x0)

这可以解决在x 0 点的增量：

δx^i = — H^{ij}(x0) d_j y(x0)

其中具有较高索引的H ^ { ij }是 (a (0,2) tensor) Hessian的逆：

H^{ik} H_{kj} = I^i_j

换句话说，理想的增量是Hessian乘以（负的）梯度的倒数。

“学习率”实际上是一个张量。

当然，在每一步中计算O（D 2）Hessian和O（D 3）的倒数在计算上是一种痛苦，但一种方法可能是每隔几个epochs做一次，并假定相同的二次近似在该持续时间内保持良好。

有没有可以简化的情况？是否有某种意义上的变量可以被认为是相互“正交”和“normalized”的？是的，但唯一的衡量标准来自Hessian本身！如果我们知道Hessian至少近似对角线并且其特征值近似相等，那么我们可以计算其行列式的D- th根，并且我们得到Hessian

H^{ij} = (detH)^{-D} diag(1,1,1 …)

这是使用Hessian行列式的逆D- th根作为标量学习率的理由。

然而，计算行列式仍然几乎是O（D 3），所以我们没有获得任何计算简单性。

,