数学比较负整数的大小（全体正整数之和为负数）

编者注：数学史上最引人注目的一个公式，是欧拉发现、后来又为印度天才数学家拉马努金重新发现的下述结果：

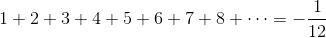
是的，你没有看错！这是一个可以讲通的公式，而且有人称之为“科学中最引人注目的公式”。

拉马努金在他的笔记中推导了这个奇妙的公式

这里的 1 2 3 … 并非我们通常所理解的无穷和，当赋予它一个恰当的含义(重新定义）时，就得到了一个负数。数学家并没有疯狂，只是不恰当地用了旧的记号。要理解它， 就需要黎曼的 zeta函数！例如，你进一步可以得到所有正整数的平方和、四次方和、六次方和等等，都等于0。

今天我们就来看日本著名的理论物理学家大栗博司是怎样来给中学生和大学生介绍这个神奇公式的证明的。以下段落取自大栗博司的科普名著《超弦理论》（一本极好的科普书，作者大栗博司的好几本科普书都有中译本，很受读者欢迎，除了本书，还有《用数学的语言看世界》、《引力是什么》、《强力与弱力》）之附录。感谢图灵教育授权本号发表。——林开亮

◆◆◆

①

这是在第四章中登场的欧拉公式，它是无数个正整数相加得到负数结果的奇怪等式。下面我来介绍一下这个公式是如何求得的。

我将列举中学水平和大学水平两种推导方法。

中学数学的推导

首先介绍一下用中学数学推导的直观方法。因为这是一种冒险的计算，所以注重数学严密性的人也许会觉得“这个方法有些不严谨”。我会在后半部分，为这些读者做出更精确的推导。

首先，我们使用中学的代数，创建下面的等式。

只要把括号打开依次展开后，正负的x的1次方、2次方、3次方就会相互抵消，因此如果等式左边的右侧括号内加到x的n次方，那么等式右边就会剩下x的（n 1）次方这一项。即：

在该等式中，假设-1<x<1，只要不断增大n的值，右边的

中的

就会变小，当n增大到无穷大的极值，它将变成 0。于是，

这里的

是x的乘方无限相加下去的意思。这个等式两边同时除以（1-x）后就变成了下面的等式。

②

接下来，等式左边的2次方将是

依次展开后将变成1个x的0次方、2个1次方、3个2次方、4 个 3 次方……即：

然后，等式②右边的2次方，与之相等。即：

懂微积分的人应该知道，即使将等式②两边x进行微分，也会得到相同的等式。

欧拉假设上述等式中的x=-1，这就刚好打破等式②的前提条件“-1<x<1”，因此这是一种违规的做法。但是，经过这种尝试也发现了某些事实。当x=-1时，得到了以下的等式。

③

虽然数字的绝对值不断变大，但是由于正负符号的存在而相互抵消，最终得到了

这个答案。在数学中，这样的做法叫作“条件收敛”。

从数字的排列看，这个计算寻求的答案一目了然。如果将左边的负号都变成正号的话，就变成了“1 2 3 4 5 6 …”。

在等式③的左边，因为偶数位的数字前面是负号，所以将其变成正号后，就把应该减去的数字相加了。因此为了纠正这个错误，如果 我们将偶数位的总和扩大到 2 倍，就应该与原来的等式相等。即：

又因为

因此

因为这个等式与等式③的右边相等，所以两边都除以-3 后，将得到下面的等式：

这样我们就推导出了欧拉公式①。

大学数学的推导

但是，上述这种推导是不够严谨的。接下来，让我们用大学的解析开拓对其进行解释说明。然后再解释为什么中学数学的推导也是正确的。

为了更好地表述无限相加，让我们来看一下复数s的函数。

④

只要s的实部比1大，这个和就是一个有限的值。例如：

这个函数的计算是由17世纪的意大利数学家提出的，当时的顶尖数学家相继向其发出挑战，但都以失败告终。一个世纪以后，欧拉发现这个无限和等于6，当时28岁的他因此一举成名。

1859年德国的数学家波恩哈德·黎曼（Bernhard Riemann）发表了题为“在给定大小之下的素数个数”的论文。他想到了这个函数的解析开拓，阐明了的值与

的值之间的关系。只要使用黎曼的关系式，即使s的实部比1小，也能够计算的值。因此，这个函数被称为黎曼的

函数。

根据等式④，我们想要计算的 1 2 3 4 5 … 为

，它与

的关系符合黎曼的关系式。因此，如果使用欧拉的成名作

，就会得出

的结果。

另外，黎曼的是为了调查质数的分布。在他 1859 年发表的论文中，黎曼提出了关于性质的一个猜想。黎曼的这个猜想尚未被证明，它是基础数学最重要的课题之一。大卫·希尔伯特（David Hilbert）于1900年提出的23个问题，以及克雷数学研究所于 2000 年公布的千禧年大奖难题都收录了这一课题。

为什么“中学数学的推导”是正确的

当我们使用中学数学推导欧拉公式的时候，会出现无穷大的问题。即便如此它仍然正确的理由如下。让我们再想一个与刚才定义的函数相似的函数。

只要s的实部大于1，和就都是有限的值。这时，模仿中学数学的推导方法，就变成了下面的形式。

在这个算式中，只要s的实部大于1，在数学上就是严谨的。一般情况下，两个函数之间的关系即使经过解析开拓也不会发生改变。因此，当s的实部比 1 小的时候，解析开拓后的和之间也同样符合上面的关系式。如果关系式中的s=-1，就变成了中学数学推导出的等式。

由此可见，计算与刚才完全相同，不同的是s的实部比1大，和为有限的值时，推导出了关系式。和

的关系也可以通过解析开拓而推导出来。因此，中学数学的推导是正确的。

好玩的数学

mathfun

↑

好玩的数学以数学学习为主题，以传播数学文化为己任，以激发学习者学习数学的兴趣为目标，分享有用的数学知识、有趣的数学故事、传奇的数学人物等，为你展现一个有趣、好玩、丰富多彩的数学世界。

↓

点阅读原文，购买【宇宙三部曲】。

,