点与世界 点与空间续三

话题：#科学# #数学# #点集拓扑#

小石头/编

---

生活经验告诉我们，苹果可以吃完，在吃苹果时，每一口咬下苹果的一部分，若 用A表示苹果，用ℰ表示全体口，则 “吃完” 是指，

• ℰ覆盖A，即，Uℰ⊇A；

每一口，吃下的是口腔中的容纳，并不包括口腔壁，也就是口腔的边界，所以 每一口 都是一个 开集，即，

• ℰ由开集组成，即，ℰ⊆τ（τ 是拓扑）

称这样的 覆盖为 开覆盖。

另外，“吃完” 还有时间限制，不能无休止的 吃下去，也就是说，还要求，

• ℰ有限，即，ℰ是有限集合；

至此，所谓的 "A被吃完" 的精确含义是：存在A的一个有限开覆盖。

我们不能保证，每一口只咬到苹果，而不吃苹果旁边的空气，也就是说：

对于任意 E∈ ℰ，不能保证 E⊆A；

所以上面才是 Uℰ⊇A ，而不是 Uℰ=A。

看到这里，爱抬杠的朋友，肯定会说：

也没有要求，每口一定要吃到苹果，可以只吃空气呀！这样以来，在吃苹果的过程中，穿插无数次的 只吃空气，使得 ℰ是无限的了。

没错！但是这样得到的 ℰ虽然是无限的，可是只要将这些无效的口删除，剩下的依然是有限的，也就是说，

• 对于A的任何开覆盖 ℬ，都存在 ℬ⊂ℰ 使得 ℬ 有限覆盖 A （即，ℬ 是 A 的一个 有限子覆盖）；

这个性质 被称为 紧致的（或 紧的）。

---

考虑 紧致的 拓扑空间 X 中任意 无穷点集 A ，假设 X 中的 每一个点 x 都有 一个 开邻域 B，只含有 A 的有限多个点，则，这些 B 组成的集合ℬ 含有 X 的每一个点，故是 X 一个开覆盖 ；

但是，ℬ 的任意有限子集只能覆盖 A 的有限多个点，从而不能覆盖全部 A，当然也就不能覆盖 X；故，X不是紧的，矛盾！所以：

X 中一定含有 一个点 x 它的每个 开邻域 B 都含有 A 的无穷多个点。 ①

再考虑 X 中 的 任意 序列 {an}；如果 {an} 是 有限点集，则必然存在 一个点 a，对于任意 N，都存在 i > N , 使得 a = aᵢ, 于是 {a, a, ...} 是 {an} 的 子序列，并且 {a, a, ...} 的极限是 a；

如果 {an} 是 无穷点集，则根据①，存在一个点a，它的任意开邻域 都包含 {an} 的无穷多个点，此时如果 X 是第一可数的，则，根据续篇知识，我们可以构建 a 的一个开邻域塔，U₁ ⊃ U₂ ⊃ U₃ ⊃ ... 由于 它们都是包含 {an} 的无穷多个点，所以 我们可以从每个 Uᵢ 中找到 一个 anᵢ 使得 nᵢ > nᵢ₋₁ ，这样就得到 {an} 一个 子序列 {anᵢ}，并且 它的极限就是 a；

综上，

• X 的任何 序列 都存在 收敛的子序列；

这个性质 被称为 列紧的。

---

上面的分析说明：

• 紧致的 第一可数拓扑空间 一定是 列紧的；

但是反过来，列紧的 第一可数拓扑空间，就不一定是 紧致的，为此 我们可以 将 第一可数拓扑空间 升级到 度量空间 来看看。

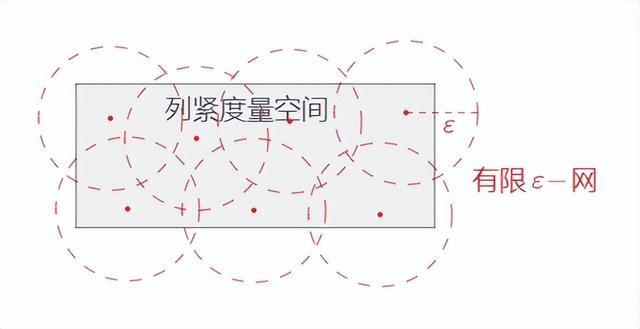
对于 度量空间 来说，可以考虑 用 半径相同的 开球去覆盖它，我们称这种覆盖为 网。对于 球半径为ε（>0）的网，我们只需要确定每个球心位置即可，于是称 球心点的全体 为 ε-网，即，

• 对于 度量空间 X 中 的点集 A，若 存在 ε>0 使得 Ux∈A B(x, ε) ⊇ X，则 称 A 是一个 ε-网；

如果 对于 某个ε， X 中不存 有限的 ε-网，则，

• 可在 X 中任选一个点 {x₁}，由于 {x₁} 不是 ε-网 ，于是 可以任选 x₂ ∈ X\B(x₁, ε) ，组成 {x₁, x₂}，显然有 B(x₁, x₂) > ε；
• 由于 {x₁, x₂} 不是 ε-网，故 可任选 x₃ ∈ X\(B(x₁, ε)∪B(x₂, ε))，组成 {x₁, x₂, x₃}，满足 B(xᵤ xᵥ) > ε，1≤u≠v≤3；
• ... ...

这样我们就得到了一个 序列 {x₁, x₂, x₃, ...} 其任意两项的距离都大于 ε，所有它不存在 收敛的子序列，进而 X 不是列紧的。也就是说：

• 度量空间中，若 某个 有限的 ε-网 不存在，则它一定不是 列紧的；

其逆反命题就是：

• 如果 度量空间 是列紧的 则 任何 有限的 ε-网 都存在；

另一方面，

• 列紧的度量空间X上的连续函数f: X → ℝ 必然有界，而且存在 最大最小值；

原因是：

我们可在 X 中找到一个序列 {xn} 使得，

limn → ∞ f(xn) = sup f(X) （注：这里允许 sup f(x) = ∞）

因为 X 是列紧的，故 {xn} 存在收敛的 子序列 {xnᵢ} ， 不妨设，

nᵢ → ∞, xnᵢ → a；

而 f 又是连续的，于是有，

xnᵢ → a, f( xnᵢ ) → f(a)；

进而得到，

limnᵢ → ∞ f(xnᵢ) = f(a)

根据 度量空间中 极限的唯一性，最终得到，

sup f(X) = f(a) < ∞

即，f(a) 是 f 最大值，f 有上界。

同理，f有下界和最小值。

对于度量空间 X 的任意 开覆盖 ℰ，可以构造如下函数，

f(x) = sup {d(x, Eᶜ) | E∈ℰ}

其中，两个 集合 A 和B 之间的距离 为它们的所有点彼此之间距离的最下值，即，

d(A, B) = inf {d(a, b) | a ∈ A, b ∈ B}

注：本文中的 最小值 和 最大值 准确的说应当是 下确界 和 上确界，这里是为了科普方便才使用大家熟悉的概念。

于是 d(x, Eᶜ) 就是 从 x 走出 E 需要的 最短距离，当然 这要保证 x ∈ E，才有意义，否则 x已经在E之外了，距离总是 0；进而 f(x) 就是 x 走出 包含 x 并边界离 x 最远的 那个 E 所需的 最短距离，也就是说 x 走出 所有E的包围，至少需要的距离。

当 y → x 时， 边界距离 x 和 y 最远的 E 总会是同一个，这时 如果假设 |f(x) - f(y)| > d(x, y) ，不妨设 f(x) > f(y) ，则有，

f(x) > f(y) d(x, y) > d(x, b)

这显然与 f(x) 的 最短要求 矛盾，故假设不成了，有，

• |f(x) - f(y)| ≤ d(x, y)

这说明 y → x，f(y) → f(x)， f(x) 连续。于是根据 上面结论， 当 X 列紧时， f(x) 存在 最小值 L （称为 勒贝格数），也就是说，当 0< ε ≤ L 时，对于每一个点x，都一定有一个 E，让 x 走不出去，即 B(x, ε) ⊆ E。

又，此时存在 一个 有限的 ε-网 A，故对于 每个 x ∈ A，都有存在 E 使得 B(x, ε) ⊆ E，这些 E 组成 ℰ 的一个 子集 ℬ，有用 A 有限 故 ℬ 有限，而 A 覆盖了 X 故 ℬ 也覆盖了 X。这样对于任意 X 的 开覆盖 ℰ，我们就找到了 一个有限的子覆盖，故 X 是 紧的。

这 说明，列紧的度量空间 一定是 紧致的；而 度量空间 一定是 第一可数的拓扑空间，于是 紧致的度量空间 一定是 列紧的，这样以来就有，

• 度量空间紧致 当前仅当度量空间列紧。

---

写个《数学分析》的朋友一定还记得，关于实数ℝ的连续性，我们总结出了如下7条等价原理：

• 戴德金性：∀ X ,Y ⊆ ℝ， X ≤ Y ⇒ ∃ c ∈ ℝ，X ≤ c ≤Y；
• 上（下）确界性：有上（下）界，必有 上（下）确界；

• 阿基米德性：∀ n ∈ℕ₊ , x ∈ ℝ ⇒ ∃! k, (k-1)n ≤ x ≤ kn；
• 完备性：基本列都是收敛列；
• 闭区间套引理（柯西-康托尔原理）：任意 闭区间套 I₁ ⊃ I₂ ⊃ I₃ ⊃ ⋯ ⇒ ∃! x ∈ ℝ , {x} = ∩ Iᵢ；
• 有限覆盖引理（博雷尔-勒贝格原理）：闭区间的任何开覆盖都有有限的子覆盖；
• 极限点引理（波尔察诺-魏尔斯特拉斯原理）：每个无穷有界集至少有一个极限点（也就是 聚点）；

显然，紧致的概念来自于 有限覆盖引理，而 极限点引理来 出自如下定理：

• 闭区间的中的任何序列都有在该区间内收敛的子序列；

因此，列紧的概念 来自于 极限点引理。

当然，以上这些等价原理只有在 ℝ 中有效，离开 ℝ 就不一定了，例如：

有限覆盖引理 在 ℝ 中 等于,

• 闭区间是紧致的；

而 在 度量空间中 可改为，

• 有界闭集是紧致的；

但 在拓扑空间中，因为没有 有界的概念，所以 不成立。不过有，

• Hausdorff 空间 中 紧集 一定是 闭集；

---

（好了，续三 就写到这里！关于 紧致 和 列紧 的概念，是比较抽象的，小石头已经尽量写得通俗易懂了，希望大家可以看懂！其实，这部分 还有很多知识，例如：加细、仿紧 等，这里 为了不喧宾夺主，就没有科普给大家，以后有机会再补上。)

,