一分钟学会数学的方法（审视几种数学解题方法中的美的元素）

数学家克莱因说：“数学是人类最高超的智力成就，也是人类心灵最独特的创作。音乐能激发或抚慰情怀，绘画使人赏心悦目，诗歌能动人心弦，哲学使人获得智慧，科学可改善物质生活，但数学能给予以上的一切。”的确，数学是一门独特的科学，数学中包括着许许多多美的因素，教师要使数学课堂教学得到预期的良好效果，让学生学得津津有味，那么，充分挖掘数学中的美育因素，用春风化雨般的艺术美使学生受到潜移默化，甚至使学生热爱数学达到如痴如醉、废寝忘食的程度，让学生在轻松愉快的氛围美之中获取知识，在精湛艺术般的课堂布局中得到美的艺术享受，所有这些蕴含于数学中的美学因素，就起着举足轻重的重要作用。

历史上许多学者、数学家对数学美从不同的侧面作过生动的阐述。普洛克拉斯早就断言：“哪里有数学，哪里就有美。”亚里士多德也曾讲过：“虽然数学没有明显地提到善和美，但善和美也不能和数学完全分离。因为美的主要形式家是“秩序、匀称和确定性”，这些正是数学研究的原则。”

我国著名数学家华罗庚说过：“就数学本身而言，是壮丽多彩、千姿百态、引人入胜的……认为数学枯燥乏味的人，只是看到了数学的严谨性，而没有体会出数学的内在美。”数学家徐利治说：“作为科学语言的数学，具有一般语言文字与艺术所共有的美的特点，即数学在其内容结构上和方法上也都具有自身的某种美，既所谓数学美。数学美的含义是丰富的，如数学概念的简单性、统一性，结构关系的协调性、对称性，数学命题与数学模型的概括性、典型性和普遍性，还有数学中的奇异性等等都是数学美的具体内容。”

我们来看看数学方法中的美。

1.反证法

我们要证明一个观点A是正确的，但是通过直接的、正面的证明不好办，比较困难，那么我们就证明与观点A相矛盾的、完全相反的观点B是错误的。通过否定观点B来反向证明观点A是正确的。

要证明观点B是错误的，常常用到归谬法，就是先假定观点B是正确的，然后根据观点B加以引申、推论，得出荒谬可笑的结论、得出违背生活常识、违反已知真理、与实际情况不符、自相矛盾的结论。从而否定观点B。

在大多数情况下，例如在检验避孕药的副作用、莎士比亚的头韵修辞法、《托拉》能预测未来等问题时，我们需要证明的是零假设不成立。做出一个与我们的预期目标相反的假设，从逻辑上讲，似乎有循环论证的嫌疑。

关于这个问题，我们其实无须担心，它是始于亚里士多德并经过时间检验的论证方法，叫作反证法或归谬法。反证法是数学领域的柔道，为了证明某个命题不正确，先假设该命题为真，然后借力打力，通过一个“过肩摔”来完成证明。如果结果是错误的，那么该假设必然是假命题，其思路为：

•假定假设H为真；

•根据H，某个事实F不成立；

•但F是成立的；

•因此，H不成立。

反证法是一种推理工具，我们对这种工具的使用已经得心应手，以至于我们都忘记了它的强大作用。实际上，毕达哥拉斯在证明 2 的平方根是无理数时，借助的就是这种非常简单的反证法。这个证明方法完全颠覆了传统，令人震惊的同时也让人们对它的始作俑者爱恨交加。它的证明过程十分简单、精炼，即使全部写出来也用不了多少篇幅。

因此根号2是有理数这一假设是错误的，即根号2是无理数。

可以看出反证法是一种很简便有效的证明方法，可以避免对直接目标来说是不必要的一些细节。而且，有一些定理，至今除了反证法以外还不可能给出与之相比更简单的证明。比如，下面这个由两千三百多年前古希腊著名数学家欧几里得给出的证明。

求证：质数有无穷多个。是否感觉头大？其实证明方法非常简单。

证明：假设存在有限多个质数，那么可以将它们一一列出：2、3、5、7、11、……、P，其中P 代表最大质数。此时，令N=2×3×5×7×……×P＋1，显然N大于上述列表中的任何一个，并不存在于列表中，所以N不是质数，这样N必须能被某个质数整除。即2、3、5、7、……、P中有一个质数Pi，可以除尽2×3×5×7×……×P＋1。然而，因为Pi是2、3、5、7、……、P中的一个，N除以Pi将肯定余1，即N不能被有限质数列表中的Pi整除，所以N是质数，于是得出矛盾。由此证明质数有无穷多个。

注：质数也称素数，是这样的一个正整数，它除了1和自身以外，没有其它的数能除尽它，比如37和43就是质数。

20世纪英国数学家G.H.哈代在其专著《一个数学家的自白》中写到：“这个定理（注：指质数有无穷多个），……毫无疑问它们是最高水平的定理。自发现之日至今，永葆其生机与效力，两千年岁月没有使它产生一丝陈旧感。它的叙述和证明，任何一个有理解能力的读者一个小时就可以掌握，不管他的数学知识是多么地少。”数学家柯朗在《什么是数学》一书中曾写到：“最近有一些卓越的数学家鼓吹从数学中完全排除所有非构造性的证明（注：主要指的是反证法）……，但这会部分地破坏富有生命力的数学整体。”

例2．（抽屉原理）3个苹果放进2个抽屉中，至少有1个抽屉中有两个苹果。

（反证法易得）10本书，共3类（抽屉），文学类（A）、史学类（B）和数学类（C），证明至少有一类有4本或4本以上。

10本书，共3类（抽屉），文学类（x）、史学类（y）和数学类（z），证明x,y,z至少有一个大于或等于4。抽象为一个纯数学问题：

假设人类的头发最多为200万根，那么某市至少有2人的头发根数一样多。（某市人口超过200万）。在任意6人中，一定可以找到3个相互认识，或3个相互不认识的人。

以上例子表明：反证法能够说明许多有趣的现象。给我们带来了美的享受：精美和优美。

2. RMI方法

中国数学教育三座学术高峰之一的徐利治教授是我国数学方法论研究领域的开拓者，其提出的RMI（关系-映射-反演）方法、数学抽象方法和数学抽象度分析方法，以及数学美学方法，都是对中国数学方法论研究有着巨大贡献，

RMI：R-relation, M-mapping, I-inversion. 即关系、映射和取逆。它属于形式逻辑范畴。如“三段式”给人以逻辑美。RMI方法体现了辨证思想的方法。Galileo(伽利略)说过：给我空间、时间和对数，我即可创造一个宇宙。

3． 抽象方法

抽象=枯燥乏味?语言学抽象吗? 美、神、好；文学抽象吗？诗歌；艺术抽象吗？绘画、舞蹈；音乐抽象吗？高山流水、悲欢离和。这些都都可以给我们美的感受。数学的抽象美的表现形式不同，它给人带来的是简洁、明快和高效的美。

点线图——拓扑学topology:

溯及历史的话，拓扑学一词诞生于19世纪初，但目前很多人认为，第一次发现拓扑学概念的人，应该是是活跃于18世纪的超级数学家欧拉，因为欧拉曾经对著名的“七桥问题”进行过深入思考。在18世纪，东普鲁士的柯尼斯堡中心流淌着一条波浪宽的大河，在河的中心则是教会，教会是人们常去的地方，所以对于当地老百姓来说，要想去往教会，就必须途径周围七座桥中的一座。天天走天天走，柯尼斯堡人民就产生了一个深深的疑问，那就是能不能经过每座桥各一次，然后又回到原来的位置呢？

例6（七桥问题）如图，能否从某个桥出发，走过所有的桥，但每座桥只

经过一次？

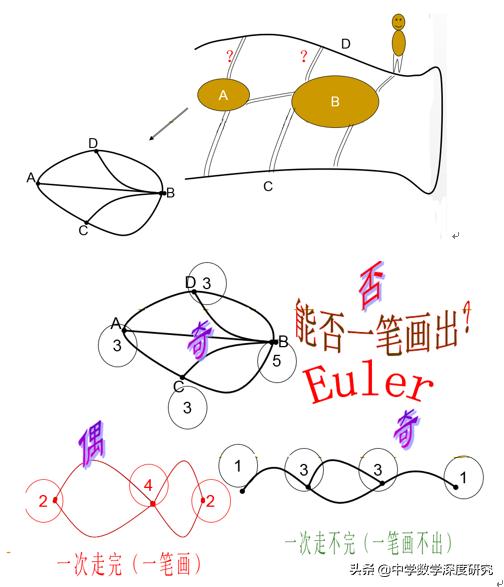
对于这一问题，欧拉证明出，如果不从所有点都延伸出偶数条线的话，就无法返回一笔画的起点。而在七座桥的简化图中，所有的点都延伸出了奇数条线，也就是说，经过每座桥各一次并回到原来的位置是不可能的。可见，欧拉就是在保持问题本质的基础上，将图形进行变形，这正是运用了拓扑学的思想将问题简化，并进而从数学角度来对问题进行解答。好了，时间凑合差不多了，那么究竟什么是拓扑学呢？

拓扑学其实是几何学的一种，几何学我们都熟悉，它是研究图形的数学，而在几何学的世界中，将什么样的图形以什么样的规则分类是很重要的。比如说，在中学数学中，全等和相似就是以边长与角度为基准来给图形分类，当然了，拓扑学并不重视这些性质。拓扑学中重要的是图形的“连接方式”，如果保持原有的连接方式来对图形进行变形，那么不管它变成成么样的，在拓扑学中，这都是同样的图形，这被称为“同胚”，所以从这一点看，大写字母A与大写字母R是一样的，因为A和R中都有两个点，这两个点都存在三条分叉，而A和P以及A和H，显然就不是同样的图形了。

总结一下，基于拓扑学的思考方式，连接方式相同的图形都被视作相同的图形，而所谓的连接方式相同，简单来说就是通过伸缩变形可以变得一样的图形。拓扑学中的变形既不能切断，也不能随意连接。

说起拓扑学，就不能不提到一个十分重要的猜想，这就是“庞加莱猜想”。庞加莱猜想的表述是这样的：任意单连通的、封闭的三维流体与三维球面是同胚的。典型的不是人话。我估计咱们能听懂的，也就是这个同胚了，如此看来，这个看不懂的猜想，应该是基于拓扑学的思考方式，认为两个东西是相同的形状。那么这两个东西，也就是单连通的、封闭的三维流体与三维球面，都是什么呢？我尝试给你解释一下，我姑妄言之，你姑妄听之，我说的我也不懂，你能不能听懂就看造化了。

首先需要明确的是，这个封闭的三维流体与三维球面，并不属于我们所熟悉的、由长宽高构成的三维世界。事实上，它们指的是更高维空间中的物体。而在我们的世界中，一切三维物体的表面，其实被称为“封闭的二维流体”，而它们之所以可以被视为三维，是因为它们可以被二维的面所封闭起来。同样的，球体的表面就被称为二维球面。那么单连通的、封闭的二维流体，指的就是没有空洞的立体表面。比如铅球、没有把手的杯子、铅笔等等，通过刚才说的拓扑学我们知道，这些物体都是同胚的。可见在我们的世界中，单连通的、封闭的二维流体，与二维球面是相同形状的。于是庞加莱就猜想，在更高维的世界中，情况也是相同的。那么到底是不是相同的呢？

强调说一下，拓扑学不注重数量关系和形状特征，而注重点与点的连接方式！如：建立校园网络系统。从网络中心到各办公楼、教学楼、学生宿舍楼，到各办公室、教室和寝室。你如何设计呢？你需要建立一个网络的拓扑图即可。实际上如果两个图的点与连接方式一致，它们实际上就是拓扑意义下的一张图。

拓扑学的产生与发展进一步表现了数学的抽象程度，起抽象的美与实际是如此的协调，展示了数学的优美！拓扑学的产生极大冲击了直观性原则！人的认知能力(直观，抽象飞跃);直观与抽象在认识上的统一受年龄和知识的接受方式的限制;直观可能造成错觉.思辩的作用越来越大,直观具有较大的局限性. 物理学、化学、生物学等学科中许多重大发现和突破是由想象力开导的。 善于抽象不仅只限于数学，人文科学、社会科学，更越来越抽象，只不过给人的感觉不象数学强烈而已。

,