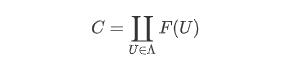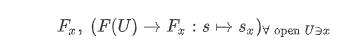高等数学中的法则（谈谈数学中的层）

话题：#数学# #范畴论# #层论#

小石头/编

前一篇，我们引入了预层的概念：

设 X 是 一个 拓扑空间（topological space）（即，规定 一些子集是开集 的 非空集合），若 F 使得，

• 对 X 中的 每个 开集 U，指定 一个 截影（section） 集合 F(U)；
• 对 X 中的 每个 开集关系 V ⊆ U ，指定一个 限制（restriction）映射 rᴜᴠ: F(U) → F(V)，并满足：
• 对于 任意 开集 U，有 rᴜᴜ = idF(U)；
• 对于 任意 开集关系 W⊆V⊆U，有 rᴠᴡ ∘ rᴜᴠ = rᴜᴡ，即，下图交换，

则 称 F 为 X 上的 集合的 预层（presheaf）。

本篇我们将介绍与预层相关的最重要概念——茎。

——§ 起 §——

给定 X 中的一点 x，考虑 X 中 包括 x 的开集的 全体 Λ，我们发现 Λ 在包含关系 “⊇” 下满足：

• 自反性：任意 U ∈ Λ ，有 U ⊇ U；
• 传递性：任意 U,V,W ∈ Λ ，若 U ⊇ V 并且 V ⊇ W， 则 U ⊇ W；
• 有向性：任意 相交的 U,V ∈ Λ， 存在 W ∈ Λ，使得 U ⊇ W 并且 V ⊇ W；

称 这样的 Λ 为 有向集 （directed set），而 Λ 通过 F 作用 得到，

(F(U))U∋x , (rᴜᴠ)U⊇V∋x

这 被称为 正向系 （direct system）。

注：如 Λ 这样，元素被用作下标 的集合，称为 指标集。

将 有向集 和 正向系 画成示意图，进行对比，

我们自然会想到：可以找，

• 一个集合 A 与 x 对应，一组 映射 σᴜ: F(U) → A 与 U ∋ x 对应；

使得 上面 右图交换，即，

• σv ∘ rᴜᴠ = σᴜ；

称 这样的 A, ( σᴜ)U∈Λ，为 正向系 的一个 目标（target）。不过遗憾的是，这样的目标显然不止一个，为了给x找一个唯一的确定目标相对应，我们 可通过 泛性 来进行筛选：

一个目标 A, ( σᴜ)U∈Λ ，若 满足，

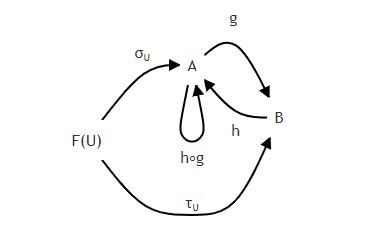
• 泛性（universal property）：任意 目标 B , (τᴜ)U∈Λ ，都存在 唯一映射 g: A → B， 使得 对任意 U ∈Λ，有 g ∘ σᴜ = τᴜ，即，下图交换，则 称为 正向系 的 正向极限（direct limit）。

虽然，这样筛选出来的 正向极限，仍然不是唯一的，但是 正向极限 有如下性质：

• 任意 两个 正向极限 都 自然同构（naturally isomorphic）；

证：若 B 也是 正向极限，则 存在 唯一 h: B → A ，满足B到A的泛性： ∀ U ∈Λ, h ∘ τᴜ = σᴜ ，于是有如下交换图，

进而 h ∘ g : A → A 就 满足 A到自己的 泛性：∀ U ∈Λ, (h ∘ g) ∘ σᴜ = σᴜ ， 有如下交换图，

而我们知道 idᴀ : A → A 也满足泛性：∀ U ∈Λ, idᴀ ∘ σᴜ = σᴜ ，于是 根据唯一性，只能是 h ∘ g = idᴀ。

同理可证 g ∘ h = idʙ，这说明 g 和 h 互逆，是双射，于是 A ≌ B 。 ▉

因此，在 同构意义下 正向极限 唯一，我们不再区分它们，记为，

称 Fₓ 为 预层 F 在 x 点处 的 茎（stalk），并 称 其元素 为 芽（germ）。

注意：上面 定义的是 集合的预层上的茎，对于 Abel的预层来说，我们还额外要求，

• 目标 A, (σᴜ)U∈Λ 中，A 必须是一个 Abel群，而 每个 σᴜ 也必须是 群同态。

另外，层就是预层，因此 层上的茎 定义，就是 预层上的茎 的 定义不变。

——§ 承 §——​

以上仅仅是从理论上，给出了茎的定义，但是要证明其存在性，我们必须实实在在的从 一个预层中将其构造出来，为此，可以 考虑，

其中 ∐ 表示 无交并 （disjoin union），指的是：

• 不同 F(U) 和 F(V) 中的 同一个元素 s 在 C 中被视为不同的元素；

注：无交并 具体实现 可以用 序对 加以区分，即，

∐ F(U) = {(s, F(U)) | ∀ U ∈ Λ, ∀ s ∈ F(U) }

但一般来说，我们依然将 C 中的元素写成 s 而非 (s, F(U))。

可以在 C 上定义关系，

• s ∈ F(U)) ∼ t ∈ F(V)) := ∃W ∈ Λ，W ⊆ U, V，rᴜᴡ(s) = rᴠᴡ(t)；

这是一种 等价关系，因为它满足，

• 自反性：rᴜᴜ(s) = rᴜᴜ(s) ⇒ s ∼ s；
• 对称性：s ∼ t ⇒ rᴜᴡ(s) = rᴠᴡ(t) ⇒ rᴠᴡ(t) = rᴜᴡ(s) ⇒ t ∼ s；
• 传递性：s₁ ∼ t ∧ t ∼ s₂ ⇒ rᴜ₁ᴡ₁(s) = rᴠᴡ₁(t₁) ∧ rᴠᴡ₂(t) = rᴜ₂ᴡ₂(s₂) ⇒ rᴡ₁,ᴡ₁∩ᴡ₂(rᴜ₁ᴡ₁(s)) = rᴡ₁,ᴡ₁∩ᴡ₂(rᴠᴡ₁(t₁)) ∧ rᴡ₂,ᴡ₁∩ᴡ₂((rᴠᴡ₂(t)) = rᴡ₂,ᴡ₁∩ᴡ₂(rᴜ₂ᴡ₂(s₂)) ⇒ rᴜ₁,ᴡ₁∩ᴡ₂(s) = rᴠ,ᴡ₁∩ᴡ₂(t₁) ∧ rᴠ,ᴡ₁∩ᴡ₂(t) = rᴜ₂,ᴡ₁∩ᴡ₂(s₂) ⇒ rᴜ₁,ᴡ₁∩ᴡ₂(s) = rᴜ₂,ᴡ₁∩ᴡ₂(s₂) ⇒ s₁ ∼ s₂；

这样，所有与 s 相互等价的元素 组成的集合 称为 等价类，记为 s‾，C 中的所有 等价类，将

C 完全分割，它们组成的集族，称为 商集，记为 C/∼。对于每个 U ∈ Λ 可定义映射，

σᴜ: F(U) → A , s ↦ s‾

则 C/∼, (σᴜ)U∈Λ 构成 一个 目标。

接着，我们需要验证该目标是 正向极限，直接通过定义来验证比较麻烦，我们这里引入，

正向极限判定定理：目标 A, (σᴜ)U∈Λ ，若 满足，

• 对于任意 a ∈A， 都存在 U ∈Λ，使得 a ∈ Im(σᴜ)，也就是，有 s ∈ F(U), σᴜ(s) = a； (Ⅰ)
• 对任意 U, V ∈Λ, 任取 s ∈ F(U), t ∈ F(V) 都有，σᴜ(s) = σᴠ(t) 当且仅当 存在 W∈Λ，W ⊆ U,V，使得 rᴜᴡ(s) = rᴠᴡ(t)； (Ⅱ)

则 是正向极限。

很明显，有，

• C/∼ 每个元素 s‾ ，因 C 是全体 F(U) 的无交并，故 s 必然来着 某个 F(U)，于是有 σᴜ(s) = s‾ ，条件 Ⅰ 满足；
• σᴜ(s) = σᴠ(t) ⇔ s‾ = t‾ ⇔ s∼t ⇔ ∃W ∈ Λ，W ⊆ U, V，rᴜᴡ(s) = rᴠᴡ(t)，条件 Ⅱ 满足；

因此 C/∼, (σᴜ)U∈Λ 是正向极限，于是 就有 F᙮ = C/∼，这样我们 证明了：

• 任意 X 上的 预层 F 以及 任意 点 x ∈ X 都存在 茎 F᙮；

注意：以上茎的构造过程是对于 集合上的预层 而言的，而 对于 Abel群的预层的，小石头会在后序文章中来介绍。

​——§ 转 §——​

现在，让我们来证明上面的定理，

证：设 B , (τᴜ)U∈Λ 是任意目标，对任意 a ∈ A ，利用条件Ⅰ，可取 s ∈ F(U) 使得 a = σᴜ(s) ，于是可令，

g(a) = τᴜ(s) ∈ B

这样就定义了一个A到B的 映射 g: A → B，实际上，

若 存在 另外的 t ∈ F(V) 使得 a = σᴠ(t) ，则 σᴠ(t) = a = σᴜ(s) ，于是 由条件Ⅱ，有 rᴜᴡ(s) = rᴠᴡ(t)，再 结合 目标的定义 有，

g(σᴠ(t)) = τᴠ(t) = τᴡ(rᴠᴡ(t)) = τᴡ(rᴜᴡ(s)) = τᴜ(s) = g(σᴜ(s))

即，下图交换，

所以，g 的确是单值的，是一个映射。而，对于任意 a = σᴜ(s) ∈ A， g 又 唯一满足，

g(σᴜ(s)) = τᴜ(s)

即，g 符合 正向极限 的 泛性要求，于是 A, (σᴜ)U∈Λ 是 正向极限。▉

另外，不难证明 上面定理 的 逆定理 也成立，因此 这个 判定条件 还是 充要条件。

​——§ 合 §——​

对于有些具体的预层实例，我们并不一定需要用上面的构造方法来得到 茎，例如：前面 №2 中的 常预层 Aᵪ，其茎 F᙮ = A，而 σᴜ = idᴀ，这个很容易 直接定义验证。

最后，需要说明，为了方便，很多《层论》书中，会将 正向极限的 符号隐去，即，不出现 Λ 和 σᴜ 这样的符号，而是将茎记为：

同时，上面的判定定理也改写如下，作为茎的重要性质：

• 对于 每个 芽 e ∈ F᙮ ，都存在 截影 s ∈ F(U)U ∋ x 使得 e = s᙮；
• 对于 任意两个芽 s᙮, t᙮ ∈ F᙮（s ∈ F(U)U ∋ x, t ∈ F(V)V ∋ x）有， s᙮ = t᙮ 当且仅当 存在 开集 W ⊆ U ∩ V 使得 rᴜᴡ(s) = rᴠᴡ(t)。

我们以后也使用这种标记法。

补充：

对于任意 s, t ∈ F(U)，显然有，

s = t ⇒ ∀ x ∈ U, sₓ = tₓ；

但是反过来，就不一定成立，我们只能由上面的性质Ⅱ，得出，

存在 一个 开集 x ∈ Uₓ ⊆ U 使得 rᴜ,ᴜₓ(s) = rᴜ,ᴜₓ(t)；

不过 若 预层 F 还具有 ，

• 单一性：若 存在 开覆盖 U = ∪i∈Λ Uᵢ ，使得 s 和 t 在每个覆盖子集 Uᵢ 中的限制 相同，即 rᴜ,ᴜᵢ(s) = rᴜ,ᴜᵢ(t) ，则有 s = t；

则 显然 U = ∪x∈U Uₓ 是一个满足单一性的开覆盖，于是可以得出 s = t。

附录：

这里，明确一下，拓扑空间的 定义。

非空集合 X 之所以 成为 拓扑空间 是因为 指定了 它的 全部 开子集 组成的集族 τ，当然这个指定不是完全任意的，我们要求 τ 中的开集 必须满足：

• ∅, X 是开集，即 ∅, X ∈ τ；
• 任意多个 开集的 并 是开集，即，对任意指标集 Λ，有 (∀λ∈Λ，Uλ ∈ τ) ⇒ ∪λ∈Λ Uλ ∈ τ；
• 有限多个 开集的 交 是开集，即，对于任意有限指标集 Λ ，有 (∀λ∈Λ，Uλ ∈ τ) ⇒ ∩λ∈Λ Uλ ∈ τ；

称 这样的 τ 为 拓扑结构。

---

（权且当做科普，茎的知识就介绍到这里吧！接下来是 层化，有兴趣的朋友可以关注小石头的后续文章。）

（哎，这个系列，写的实在太烂，是小石头能力不够，无法做到高屋建瓴的通俗易懂，实在是愧对大家的期望。）

,