导数不等式（利用导数证明不等式）

利用导数证明不等式

函数如果连续可导，利用导数为零的点及函数的单调性，就可以证明某些不等式。

首先复习一下预备知识。

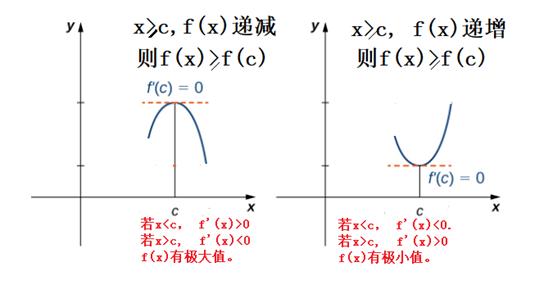
如果f(x)在c处有一个局部极值并且f(x)在c处是可导的，那么f ' (c) = 0, 反之亦然。

若f(c) 是极大值，则有f(x)<f(c); 若 f(c) 是极小值，则有f(x)>f(c)。

示例1：若x>0, 证明ln(x)≦x-1 .

证： 令f(x)=ln(x)-(x-1)

则f’(x)=1/x-1, 当f’(x)=0， 则x=1,

当0<x<1时， f’(x)>0,

当x>1时， f’(x)<0,

因此x=1, 函数 f(x)有最大值f(1)=0,

所以f(x) =ln(x)-(x-1) ≦0, 就是ln(x)≦x-1， 证毕。

示例2：若x>0, 证明1 2lnx≦x2

证：令f(x)=-( 1 2lnx)

则f’(x)= 2x-2/x-=2(-1)/x , 当f’(x)=0, x=1 (x=-1舍去)

当0<x<1时， f’(x)<0,

当x>1时， f’(x)>0,

因此x=1, 函数 f(x)=-( 1 2lnx)有最小值f(1)=0,

所以f(x) = -( 1 2lnx)≥0, 就是 ( 1 2lnx) ≦ ，证毕。