向量的向量积的应用（向量叉积的定义和应用）

如果我们把两个向量相乘，得到另一个向量它垂直于两个原向量。 这个操作就是求叉积。 我们可以用叉积求出垂直于两个给定向量的方向，求出两个向量张成的面积，确定两个向量是否正交，等等。 那么，什么是叉积呢?

两个向量的叉积得到一个垂直于由两个原向量组成的平面的向量。

什么是叉积?

首先，我们可以求两个三维向量的叉积! 这是对两个三维向量进行的运算结果是第三个向量垂直于两个原始向量，其大小是第一个向量的大小乘以第二个向量的大小再乘以两个向量夹角的正弦。

我们回顾一下向量,请参考向量的基础知识

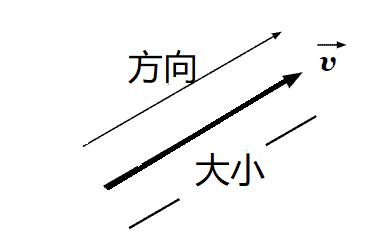
在上图中，我们有一个向量v→。 这个矢量的大小就是它的长度，矢量的方向已经显示出来了。现在，如果我们求两个向量a→和b→的叉积，其结果将是c→，如下图所示:

注意，当求叉积时，你可能会注意到两个垂直于两个原向量的方向。 向上和向下。 为了找出外积的方向，我们要用到右手定则。

用右手法则，你握住右手，食指指向第一个矢量的方向。然后，把中指转向第二个矢量的方向。举起你的大拇指。你的拇指现在应该指向叉乘向量的方向。

请注意，如果你改变向量的顺序(切换a→和b→)，叉积向量的方向将相反。 因此，叉积运算是不可交换的; 顺序很重要!

叉积的公式

正如我们提到的，外积是定义在三维向量上的。 我们可以把向量写成分量的形式，例如，取向量a→，

x分量是a1, y分量是a2, z分量是a3。 现在，让我们考虑如下所示的两个向量:

a→和b→的叉积由公式给出:

这个公式记起来有点乏味。 但是不要担心，这个公式来自于3×3矩阵的行列式。

回想一下2×2矩阵和3×3矩阵的行列式公式(请参考行列式的基本概念）。

对于二阶方阵:

行列式的值为：

对于一个3阶的方阵：

行列式的值为：

现在, 我们可以把向量a→和b→写成3×3矩阵的行列式形式，如下所示:

将其打开分离：

这就是我们刚才展示的公式!

注意:向量i→，j→和k→是标准基向量，它们必须按照给定的顺序出现。

单位向量的叉积有：

怎样计算叉积

我们来看一个求向量a和向量b，向量b和向量a的叉积的例子， 若：

求axb, 和bxa

先求axb，

我们将把这两个向量写成3×3矩阵的形式，并用已知的行列式公式计算外积。 步骤如下:

我们再求bxa:

注意，改变向量在叉乘中的顺序改变了所有符号! 这意味着这两个叉乘在方向上是相反的! 我们在上面学习右手法则时就注意到了这个事实!

向量叉积的一个重要应用是给定两个共点向量，求其形成的平行四边形面积。

首先我们要证明向量叉积的矢量长度满足以下公式：

现在我们证明这个公式，假设向量u， 和v，

让 u = 〈 u1, u2, u3 〉 ， v = 〈 v1, v2, v3 〉 ，它们的夹角为θ，那么：

所以：

因此有两个向量的叉积的模（长度）公式：

根据向量叉积定义，从上图可以看出，平行四边形的面积为：

若向量a, b分别给出， 那么它们所形成的平行四边形面积见下面的计算：

根据上面的推导，可知a, b的矢量积的模即为面积。

矢量的点积与叉积的混合积可以计算棱柱的体积， 如图：

此外，利用矢量积的叉乘，若夹角为0， 那么sinθ=0为零，即：

可以得出a, b平行的条件：

我们可以推出：

也就是：

由此推出两个向量平行的充分必要条件是：

,