函数极限存在和可导的条件（函数的极限连续）

之所以写这篇文章，目的在于缕清函数极限、连续、可导、可微内在思路，只要思路清晰了，我们才可以做到心里有理有据，大方向不出错。

函数的极限、连续、可导、可微是怎么步步为营，层层递进的。

首先我们看看极限是怎么提出来的？极限：无限靠近而永远不能到达，英文名字limit，极限符号就是取缩写lim，它就是一个符号，意思是自变量x取值靠近一个数，函数值是多少。

在计算曲线长度的时候，我们不会测量曲线的长度，只能把曲线不断分割，再把分割的线近似等于直线来测量，这样下来我们就可以得到曲线的近似长度；那怎么更加逼近曲线真是长度呢？只有切割无限多无穷小的直线才可以更真是模拟曲线长度，这里的无穷小，到底是多小呢？在数字中数学0是最小的，无穷小只有无限逼近0但不能等于0，这样才可以划分的最小，无穷小是一个动态的变化的数值，在数学中是不能计算出具体结果的，于是数学家引入一个新的数学概念---极限，无穷小的极限等于0，是具体的数值，这样我们就利用无穷小的极限来进行计算了。

为了形象表达极就是动态变化的，我们拿0.999...... 数字9无限循环下去，这个数字一直在变化，我们可以取它极限也就是1拿来计算。

为什么需要求极限，凡是涉及无穷的问题都是需要求极限的问题，因为无穷就是一个动态变化过程，不能直接求出精确数值，只能利用极限思想求值。

极限我们是可以从不同方向求取的，也就是左极限和右极限，如下图我们可以求出一段函数的左极限或者右极限。

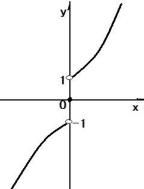
有了极限思想，那么函数的连续性就自然而然解决了，如果函数上点P，在P点可以向左移动无穷小，也可以向右边移动无穷小，那么我们就说函数在点P处是连续的，因为无穷小是任意小，只要你想到多小就有多小，中间是没有缝隙的，也就是说只有P点的左极限和右极限相等时，才能说明函数是在点P处连续的，极限唯一确定才连续。连续是不管是不是光滑，尖角也可以是连续的例如图中点b处。

有了连续概念，接下来我需要研究连续函数的光滑程度，变化方向，也就是导数，导数具有导向、向导含义，也就是表示方向的意思。导数几何意义就是在点P的切线，也就是正切值。切线就是触碰的意思，既然有方向性就有正负,具有矢量性质。要是要求函数的导数存在也就是导数是确唯一的，那上图做例子，b点左侧的到时是负值，右侧的导数是正值，从左边导数和从右边导数是不相等的，说明在b点导数是不存在的，导数是验证函数变化方向和变化光滑程度。

接下来我们看看可微，可微也就是可以划分成微小的区域，在一元函数中，也就是可以把曲线切割开来，只要足够小，划分区域就可以等同直线，这就和导数含义一致了。所以在在一元函数中，可微和可导是等价的；

但是在二元函数中，可微是把曲面划分成微小的直面，也就是平面，是以直面代替曲面进行计算，利用微平面计算。但是可导呢？可导还是一维产物，是在一个方向的变化程度，一个二维直面和一个一维直线段是不能等价。所以在二元函数中，可微和可导不是等价的。

我们来梳理一下，极限、连续、可导、可微的递进关系：

一个函数点A是可以从左边和右边两个方向求极限的，左极限和右极限可以相等也可以不相等；只有点A左极限和有限性相等的时候，我们才可以说函数在点A是连续的，连续是个标量，没有方向，也就是尖角和圆滑角都可以连续；导数是方向，切线，也是有方向的，尖角处左导数和右导数是不相等的，只有左右导数是相等的才是说明点A处可导；可导是方向是一维空间，可微是微线段、微直面、微立体等等是不同维度的，只有一维空间的位线段可微和可导是等价的，但是到微直面、微立体的可微是多维度的，不能和一维度的可导等价。