很好看的绳结（艺术中的绳结）

女士们，先生们，老少爷们儿们！在下张大少。

本文分析绳结和链接在古代艺术中的应用，从巴比伦、埃及、希腊、拜占庭和凯尔特艺术开始。我们以凯尔特艺术和安哥拉绍奎人的民族艺术或泰米尔艺术为例，分析了艺术中使用的绳结的构造方法，在这些艺术中，绳结被构造成镜像曲线。我们提出了不同的方法来生成基于几何多面体的结和链接，适用于建筑和雕塑的应用。

1. 古代艺术中的绳结

矩形网格中单线性曲线和结的一些最古老的例子是用饰片构造的:a，b ∈ N维的矩形网格RG[a，b]，其中a，b是互质数。犹如一条蛇在吃它的尾巴，这是衔尾蛇的经典象征，美索不达米亚乌尔(Ur，Mesopotamia，约公元前2600-2500年)的圆柱形印章印记显示了一条蛇，它带有交织的线圈，放置在9×5网格的RG[9，5](图1)中就是这种结构的一个例子。公元前1700年左右，安纳托利亚的印章也使用了类似的长方形或圆形格子板作为邮票印章。我们假设，在公元前3500年左右发明文字之前，以绳结和链环为图案的邮票、圆筒印章就已经出现了[1]。

图1.(A)圆筒印章，美索不达米亚乌尔，公元前2600-2500年；(B)邮票印章，安纳托利亚，公元前1700年左右。

由于纤维制品难以长久保存，今天很少有史前中国结的例子。一些最早的绳结证据保存在战国时期(公元前481-前221年)的青铜器皿、北朝时期(公元317-581年)的佛教雕刻和西汉时期的丝绸绘画上。中国结是一种装饰性手工艺品，始于中国唐宋时期(公元960-1279年)，是中国民间艺术的一种形式。后来在明朝推广开来。这种艺术也被称为中国传统装饰结(图2)。

图2：中国传统装饰结

与绳结有关的最美丽的传说出现在希腊神话中。与亚历山大大帝有关的戈尔迪乌姆之结（Gordian knot），这是西方传说中的物品，神谕说，如果谁能解开这个结，那么他就会成为亚细亚之王。亚历山大大帝上去看也不看，一刀斩断。戈尔迪乌姆之结经常被用来比喻一个难以解决的问题。虽然没有人知道戈尔迪乌姆之结的类型，但解结数是最简单的结不变量之一，但也很难计算，也被称为"戈尔迪乌姆迪数"。

最早关于外科医生吊索的研究和描述是由一位名叫Heraklas的希腊医生写的，他生活在公元一世纪。在这篇文章中，Heraklas循序渐进地解释了18种绑矫形吊索的方法。每个节点的闭合表示一个结或环(图3)。

图3. 交叉绳索的闭合，得到了绳结52

此外，从米诺斯时期开始，在希腊珠宝中可以找到海格力斯之结(图4)的绝妙例子。平结在古希腊被称为海格力斯之结，它过去和现在都被广泛用于医学上作为一种结扎结。普林尼在他的《自然史》中表达了这样一种信念：用海格力斯之结捆绑的伤口愈合得更快。

图4：海格力斯之结，希腊珠宝，庞蒂卡(乌克兰)，公元前300年

在希腊马赛克中，可以含蓄地找到艺术中绳结和链接的美丽例子。蜿蜒形状的希腊地板马赛克上的装饰是四叶图，可以被认为是结投影，通过添加一条链在另一条链上传递的信息，可以很容易地转换成相应的结和链接。例如，从纽结理论的角度来看，希腊马赛克(图5a)表示链接62,1(图5b)。

图5：希腊马赛克，可以转换成链接62,1

2. 镜像曲线

"对辫子、编织和篮子等三维艺术的模仿是交错和结绳交错设计的起源。很少有种族没有把它用作石头、木材和金属的装饰。在地中海、黑海和里海周围的大多数人、埃及人、希腊人、罗马人、拜占庭人、摩尔人、波斯人、土耳其人、阿拉伯人、叙利亚人、希伯来人和非洲部落的艺术中都可以找到交错的花环、饰带和装饰品。它们的亮点是凯尔特人的交错绳结工程、伊斯兰的分层图案和摩尔人的地板和墙壁装饰"[2]。

凯尔特结是结艺的亮点之一。一些研究人员认为，凯尔特结艺术的根源是在10 - 11世纪的东方马赛克图案的结设计，特别是波斯瓷砖。绳结艺术的最开始可能起源于从饰片构造的镜像曲线，这也被古物学家J. Romilly Allen认为是所有凯尔特结的基础，他20年的工作总结在《异教和基督教时代的凯尔特艺术[3]》一书中。

我们简要介绍了镜像曲线的构造，并在2.3节中给出了详细的说明。

基本构造使用由正方形组成的矩形网格，但可以用两种方式来概括：通过多边形和插入内部双面镜，到由边对边镶嵌组成的平面的任意区域。首先，连接相邻边的中点，得到一个4-正则图：每个顶点都入射到四条边上，称为阶梯。在这个图中，每一步只出现一次的每一条闭合路径被称为一个组件。镜像曲线是所有组件的集合。因为图是4叶的，所以在每个顶点，我们有三个选择的边来延续路径:选择左边、中间或右边。如果选择了中间的边，顶点被称为交叉点。通过引入“上下”关系，每一条镜像曲线都可以转化为一个绳结设计。

“镜像曲线”的名称可以通过假设该区域的所有外部边缘都是镜像来调整，附加的内部双面镜像放置在多边形所有其他边缘的中点，共线或垂直于边缘。为了简单起见，假设我们有一个由正方形组成的矩形网格，即平板，并且一束光以45°的角度从一个边缘中点发出。它将穿过网格，经过一系列反射后到达起点。如果整个网格没有被覆盖，我们可以通过从不同的边中点开始重复这个过程，并一直持续到使用整个阶梯图，最终描绘出一条镜像曲线。

这些设计的共同几何构造原理是由P. Gerdes发现的，即使用（两面）镜子入射到正方形、三角形或六边形规则平面拼块的边缘，或垂直于边缘的中点[4,5]。在理想的情况下，在一系列连续的反射之后，光线到达其起始点，定义了一条单一的封闭曲线。在其他情况下，结果由几条封闭曲线组成。例如，下面的镜像图案（图6）对应于G. Bain的《凯尔特艺术》一书中的凯尔特图案[2]。

图6：凯尔特结设计

从没有内反射镜的板获得的设计中的反射镜曲线的数量是板边a和b长度的最大公约数，见第2.4节。因此，如果a、b互为质数，则得到一条曲线，即一个结。有趣的是，从板上的单个曲线获得的所有结都满足使用称为李萨如结的cos函数的参数方程[6]，并且可以被重新参数化以被视为立方体内部的台球结。

对于一个任意的a≥3和b=2得到的无限系列板块，由有理数结和链接组成，由它们的康威符号[7]给出 3 1 3, 3 1 2 1 3, 3 1 2 1 2 1 3, 3 1 2 . . 2 1 3（图7）。

图7：从RG[a, 2]得到的KL，a=3, 4, 5

对于任意a≥3和b=3，我们得到具有多面体纽结和链节的板：对于a=3，我们有3分量链节8∗2：2：2：2，对于a=4，可以得到纽结1312∗: 2 0 ::: 2 0.2.2 0,，等等(图8)。

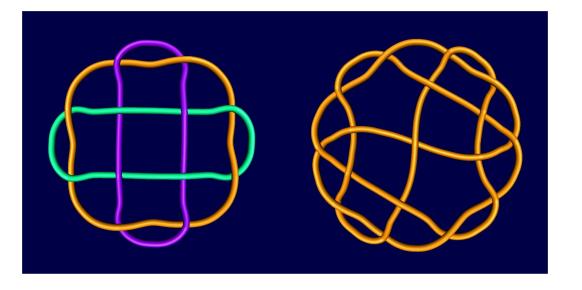
图8：从RG[a, 3]得到的KL，a=3, 4

2.1. 泰米尔地板画设计

“在玛加利收获月(12月中旬至1月中旬)，印度南部的泰米尔妇女过去每天早上都会在自家房屋的门槛前绘制图案。玛加利是各种流行病应该发生的月份。他们的设计是为了安抚掌管玛加利的湿婆神。为了准备他们的画，妇女们扫了一小块大约一码见方的地方，并在上面洒上水或抹上牛粪。在干净潮湿的地面上，他们画出了一个由等距点组成的矩形参考框架。然后，形成设计的曲线是通过将米粉夹在手指之间，通过手指的轻微移动，当手向所需方向移动时，让米粉以一条封闭、平滑的线下落而形成的。这些曲线的绘制方式是它们包围着这些点，而不接触它们”[8]。

根据泰米尔文化，理想的设计是由一条连续的线组成。由一条“永不停止”的线组成的图案通常命名为pavitram，意思是“环”或“梵天之结”(图9)。pavitram的目的是为了吓跑巨人、恶灵或魔鬼。

图9：泰米尔设计

2.2. 安哥拉绍奎人沙画

“安哥拉东北部的绍奎人以他们美丽的装饰艺术而闻名。当他们相遇时，他们会用地面上的图画来说明他们的对话。这些画大多属于悠久的传统。它们指的是谚语、寓言、游戏、谜语等。并在一代人向另一代人传递知识方面发挥重要作用”[9]。

"......就像南印度的泰米尔人一样，绍奎人发明了一种类似的记忆装置，以方便记忆他们的标准化图纸。在清洁和抚平地面后，他们首先用指尖划出一张等距的正交网。行和列的数量取决于要表现的图案。应用他们的方法，绍奎绘画专家将整个设计的记忆减少到主要是两个数字和一个几何算法的记忆。他们的大多数图画显示出双边和/或旋转（90◦或180◦）的对称性。他们的象形图的对称性促进了绘图的执行。这一点很重要，因为绘图必须顺利和连续地执行。绘图者的任何犹豫或停顿都会被观众解释为不完美和缺乏知识，并以讽刺的微笑表示赞同" [9]。

被称为sona的绍奎人沙画（图10）在将知识和智慧从一代人传给下一代方面发挥了重要作用。年轻的男孩喜欢用手指制作沙画，并听他们讲故事。他们在密集的学校教育时期，即mukanda成人礼期间，已经学会了如何制作简单的图画及其意义。更复杂的sona只有讲故事的人知道，他们是真正的akwakuta sona（懂得绘画的人），受到高度尊重，构成了绍奎社会中的精英阶层[4]。

图10：绍奎人的沙画

2.3. 镜像曲线的构造

“列奥纳多花了很多时间来设计一系列有规律的结，这样绳索就可以从一端追踪到另一端，整个绳索填满一个圆形的空间……”[2]。

莱昂纳多·达芬奇和丢勒，两位最伟大的画家/数学家，对构建绳结设计很感兴趣，与镜像曲线密切相关[2]（图11）。他们知道并非常有效地利用了这样一个事实：对于尺寸为a、b的矩形方格RG[a, b]，其中a和b互素，镜像曲线总是一条均匀地覆盖矩形的封闭曲线。

图11：列奥纳多·达芬奇的拼接

由P.Gerdes阐述的凯尔特人、绍奎人或泰米尔结设计的常见几何构造原理是使用入射到正方形、三角形或六边形规则平面拼块边缘的（两面）镜子，或垂直于边缘的中点[4,5,8,9]。在理想的情况下，在一系列连续的反射之后，光线到达其起始点，定义了一条单一的封闭曲线。在其他情况下，结果由几条封闭曲线组成。例如，以下的镜面图案（图6）对应于G. Bain的《凯尔特艺术》一书中的凯尔特图案[2]。

Gerdes的书[10,11]给出了古埃及、美索不达米亚、印度和非洲文化中镜像曲线的例子和分析，[12,13]分析了镜像曲线和矩阵之间的关系。

此外，还有一个更漂亮的几何属性：镜像曲线可以仅使用几个不同的原型获得。特别是，只有三个原型拼块足以构建所有内反射镜入射到规则三角形拼块单元边缘的反射镜曲线，5个用于正方形，11个用于六边形规则拼块(图12) [14]。

图12：从均匀拼块获得的结设计

使用来自11个均匀阿基米德镶嵌[15]的多边形的组合，或者产生空间结构印象的原型和彩色原型，我们可以获得交错的艺术图案，模块化设计的例子：使用一些初始元素(模块-原型)来创建设计的无限集合。从阿基米德镶嵌获得的镜面曲线类似于光学现象：光线从一个物理环境转移到另一个物理环境的方向变化。

正如我们已经说过的，理想的镜像曲线是一条单线曲线，由一条曲线组成，对应于一个结。单线性曲线可以从k曲线获得，k > 0覆盖了由T表示的平面镶嵌的一个区域，方法是放置内反射镜，记住它对曲线的影响。这些动作有时被称为“曲线手术”:

混合交叉：任何放在两条不同曲线的交叉点上的镜子都会将它们连接成一条曲线。

自交叉：根据其位置的不同，放置在(定向)曲线的自交点中的镜子可以保留曲线的数量，也可以将曲线一分为二(图13)。

图13：一面镜子放置在(A)两条不同曲线的交叉点上；(B)一条曲线的交叉点上。

从k曲线开始，将它们转换为单个曲线所需的最小镜像数为k-1，并且需要在混合交叉中添加。这个简单的算法显然是有限的。如果k = 1，我们有一个单一的镜像曲线，所以不需要额外的双面镜。如果分量数为k (k ≥ 2)，我们将第一个双面镜放置在两条不同曲线的交叉处，连接它们并获得k-1分量。以同样的方式继续，引入k-1反射镜后，将获得单反射镜曲线。如果我们允许在相同组件的自交叉点添加镜子，我们的游戏会变得更加有趣。这种移动既可以保留曲线的数量，也可以增加1，这样我们就可以得到一条单分量或多分量的曲线。

在尺寸为a，b的矩形正方形网格RG[a，b]的特殊情况下，在没有内部反射镜的情况下获得的曲线的初始数量等于最大公约数k = GCD(a，b)，因此，除了获得单个曲线所需的最小反射镜数量之外，我们还知道最大数量2ab-a-b。通常，我们可以使用这些规则来修改任何单线性反射镜曲线，而无需增加组件数量(图14)。

图14：在RG[2，2]中连续引入内镜，保留了一条曲线

请注意，镜像曲线的构造独立于度量属性或曲面的几何形状，因此相同的构造原理可以应用于任意曲面的任何边对边镶嵌，例如球体或双曲平面。使用添加双面反射镜的规则，任何反射镜曲线都可以在有限的步骤中转换成单个反射镜曲线(图15)，正如我们在上面描述的平面镶嵌一样。

图15。通过连接边缘中点(b)从瓷砖(a)构建单一镜像曲线；追踪组件(c)并引入镜子(d)。

2.4.镜像曲线的组合

现在让我们描述四条用于组合板设计和/或镜像曲线的一般规则。前三个规则是由P.Gerdes[5]给出的，第四个规则是由S.Jablan提出的。我们的注意力将局限于从具有全等正方形单元的多项式得到的镜像曲线。

构造规则：

1.第一条规则描述了如何组合两条镜像曲线，这两条镜像曲线在其边界上共享开放单元格的一条边(图16a)。这样的构图对应于KL的直接产物，它可能是结艺术中被利用最多的结构之一。对于给定的镜像曲线M1和M2，我们称这种直积为×-直积，记为M1×M2。如果我们以这种方式合并两条镜像曲线，第一条是c1，另一条是c2分量，结果是一条具有c1 c2-1分量的新镜像曲线。因此，两条单分量镜像曲线的×-直积是一条新的单分量镜像曲线。例如，在绍奎人的设计和许多凯尔特人的饰带中都使用了这个想法。

作为第一个规则的一个特殊应用，我们可以在任何单线性镜像曲线的边界上添加一个正方形。这种转换相当于向KL图添加一个外部循环。它不改变组件的数量，并且可以重复，因为它在扭结艺术中具有装饰功能。例如，图9a中的泰米尔(unknot)设计是通过一系列外部循环添加创建的，从RG[1，1]开始；通过在RG[4，3]上增加环，图9b中的结设计；和图9c中的结设计，在RG[5，3]上增加了环。同样的结构用于绍奎设计(图10a)。

2.第二条规则是定义结理论中的直接和K1#K2的规则（图16b）（注意，第一条和第二条规则，即镜像曲线的×-和|-积都对应于结的直接积K1#K2，但第一条有一个无用的交叉。使用镜像曲线的×-和|-积得到的结或链接与K1#K2是环境同构的，但作为结图或链接图却不是相互同构的）。在镜像曲线M1和M2的语言中，它意味着我们切断每条镜像曲线M1和M2的一条外边，并重新连接它们，得到一条新的镜像曲线，将用M1||M2表示。

3.第三个规则仅限于平板设计:两个重叠正好由两个单元组成的单线平板设计将给出一个新的单线平板设计。第三条规则的示意图如图16c所示。

4.将板设计P1添加到板设计P2是对属于直线边界的边界单元的边缘到边缘的识别(图16d)。以同样的方式，我们可以将板设计P1添加到放置在某个多项式中的某个镜像曲线M上。此操作可概括为将板设计添加到多项式中。

第四条规则告诉我们，将网格RG[a，b]中的任何设计添加到沿b的任何单线性镜像曲线M(或单线性板设计P2)上，使得b|a产生单线性设计(图16d)。特别地，任何平方RG加到单线性设计上都给出了一个新的单线性设计。

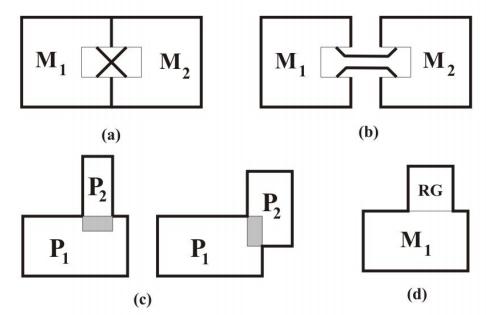
图16：版面设计和镜面曲线的构图规则

此外，将镜像曲线M2添加到单线镜像曲线M1，使得放置M2的多项式的沿边缘b的每条曲线接触点属于M2的不同分量。新的镜像曲线M1 M2将产生一条单线性曲线。

这四条规则足以创造出单线性平板设计，并将单线性从RG扩展到平板设计。额外的复杂性和多样性来自于增加内部反射镜。如图13所示。对称的镜像曲线在结绳艺术中占主导地位，因为对称性被认为是理想的视觉特性。这意味着大多数镜子的排列在美学上并不美观。例如，在RG[6, 3]的52个双镜排列中只有8个是对称的。

我们提出下面的方法来从对称的单线板设计P构造对称的反射镜曲线。首先在P的某个交叉点A放置一个内反射镜，并描绘一条定向的反射镜曲线m。现在我们有两种可能性:

1.如果我们的镜像曲线M没有完全覆盖P，则在M上选择一个与A对称的混合交叉点，并在A中放置一个与镜像对称的镜像(图17a1)。如果不存在具有此属性的对称点，请将A中的镜像围绕其中点旋转90◦，然后将镜像放置在与其对称的位置(图17a2)；

2.如果P完全被M覆盖，则在A中放置一个与该镜子对称的新镜子(图17b1)。如果单线性被破坏，请将A中的镜像绕其中点旋转90◦，然后将镜像与其对称放置(图17b2)。

这种方法被用来解释泰米尔、绍奎和凯尔特绳结艺术中出现的不同镜像曲线的构造。我们已经解释并说明了由单一的单线板设计RG通过增加一系列的外部循环而得到的绳结设计，以及作为单线板设计的直接产品而得到的设计（规则1，用×表示）。

图17：创建单线性对称镜像曲线的算法

第一条规则，即×-直积，在凯尔特人的结绳艺术中非常频繁地用于建造饰带（或花纹），以及k-直积（规则2）。它们都是获得平移重复结构、饰带，甚至平面对称组的标准工具。

应用第二条规则在两个单线性RG的角上连接起来，也就是说，它是相应结的k-直和。类似的方法是使用（或多或少）"开放"的板式设计RG和相应的镜像曲线的k-直和。虽然产生的复合结和链接是相同的，但得到的图案在视觉上会有很大的不同。

为了分析基于k-直积的凯尔特结，我们首先需要在基本(单线性)RG中插入一些垂直于边缘的内镜，以便获得凯尔特结的部分——“缠结”，并且适当地放置进出线。其位置的可能选择是基本RG的两个上角(或下角)、两个对角线(升角或降角)，或者所有四个角形成一个“缠结”。在第一种情况下，我们放置垂直于边界单元的“垂直”和“水平”边缘的内镜，形成L形形状。此外，切割设计的长边并将其重新连接，我们可以获得不同的卷边设计(基本KL的直接产品)，并适当放置进出线(图18)。

图18：凯尔特缠结

另一种可能性是从RG中创建“缠结”(图18)，并将它们组成链(或封闭的圆)(图19和20)。在绍奎人沙画的例子中，使用了类似的策略来获得“开放”RG，该RG可以进一步由k-直和或×-直积组成(图10b)，以形成更大的网络。

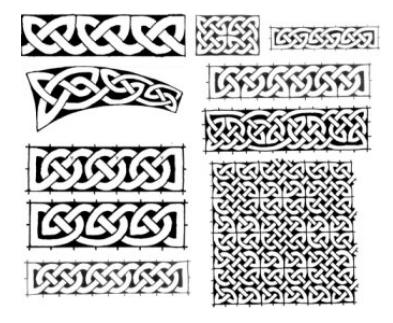
图19：凯尔特结，饰带和平面绳结饰品

图20：凯尔特圆形和方形结设计

第三条规则是绍奎沙画制作中最受欢迎的规则之一。以这种方式组成了一系列“社会性”的单线板设计，代表一只带幼崽的豹子，一个名为kambava wamulivwe的设计，代表一只死在岩石中的动物kambava(图21b)，或者一幅名为tambwe的sona绘画，代表一只狮子(图21c)。

图21：(A)绍奎设计中的k-直积；(b，c)规则3在绍奎设计中的应用。

第四条规则在饰片的形状方面提供了最高的自由度，在结绳艺术中经常产生对称的饰片（图22）。因此，我们可以构建一个完美的单线性曲线，其形状是通过添加不同的板块获得的。

图22. 凯尔特人单线交叉结设计的推导，来自于使用规则4得到的饰片设计。

创造各种单线板设计打开了艺术创造力和发挥的大门：有大量的方法可以引入内部边缘入射和边缘垂直反射镜，同时保持单线(图23-26)。

图23：凯尔特单线结交叉设计

图24：凯尔特镜像曲线

图25：凯尔特人的单线设计，打破了对称性

图26：通过打破双组件对称设计（a）的对称性，构建凯尔特人单线结设计（b）

与单线交叉结设计的显著例子（图23）一起，图25和26显示了复杂的单线结设计的有趣例子。因为同一设计的对称版本（图26a）是一个双组件的结设计，凯尔特大师通过打破对称性将其修改为一个几乎对称的单线性设计（图26b）。

3. 结绳设计的对称性和分类

P. Cromwell[16]利用镜像曲线的对称性对凯尔特人的饰带设计进行分类，而P. Gerdes[8]则对泰米尔设计进行了重建。乍一看，对称性似乎是完美曲线的构造和可能的分类的数学基础[8,14,16]，但不对称曲线的存在要求采用其他方法。

如果我们把它们当作纯粹的几何对象，我们可以强加以下等式关系：

两条镜像曲线是相等的，如果有相似性将其中一条转化为另一条。

换句话说，如果一条镜像曲线可以通过比例和等距的组合作用从另一条中获得，则它们被认为是相同的。这种关系可以用非常相似的方式在镜子排列的层次上研究。

N维欧氏空间En的变换S称为等距变换，如果对每两个点X，Y及其像X0=S(X)，Y0=S(Y)符合XY∼=X‘Y’。

一个图形f是空间的任何非空的点的子集。

如果S(f)=f，一个图形被称为对一个变换S的不变性，而S被称为f的对称性。

一个图形f的对称性形成一个群，称为f的对称群，并表示为Gf（例如，见[15,17,18]）。

空间En的等距对称群可以根据关于所讨论的群的变换作用不变的最大真(子)空间序列来分类。饰带G21、带G321、平面装饰物G2和层G32的对称组可用于结工图案的分类。等距对称群将根据结晶学符号(或赫尔曼和莫金符号)来表示。

恰好存在7个对称的饰带群、31个对称的条带群、17个对称的平面装饰群和80个对称的层群(例如，见[15，17–20])。

一个物体或图案的对称组的基本区域是该图案的最小部分，根据对称性，它决定了整个物体或图案。

在所有面向对称的交错图案的分类中，即无限的绳结图案(例如，[16]或[15])，对称性被用作分类的唯一标准。线性纽结图案按7个饰带对称群或31个条带[15，19，21]对称群分类，而不考虑它们的拓扑或纽结理论性质。同样，平面对称图案按17个平面对称组或80个对称层组进行分类。在所有这些情况下，我们都有一个非对称的基本区域乘以属于对称群的对称性，而没有考虑到基本区域可以是任何具有特殊纽结理论属性的非对称纠缠。例如，根据面向对称的分类，图27中所示的两个带将被认为是等价的，因为它们的对称群是p1a1，尽管第一个带基于作为分子闭合Hopf link 221(2)的缠结21，而另一个带是结2 1 1 2的直积。

图27. 凯尔特饰带上有相同的带状对称组p1a1。

对于无限对称交错图案的分类，我们提出以下两个准则:

1. 图案的等距对称群;

2. 缠结在基本区域内。

这些标准并不总是充分的，我们还需要考虑其他的结理论属性，如一个图案是否代表质数或复合KL排列。

如在n-缠结(n = 2，3，...)一般来说，我们可以考虑包含在基本区域中的缠结的所有可能闭合，作为进一步分类的基础。例如，通过连接具有相同对称性p121的两个饰带的基本元素的缠结的左端和右端(图28)，我们分别获得链接3#2和2 1 2，2，2 。

图28：具有相同对称组带的凯尔特饰带p121

这一分类是由S.Jablan和LJ Radovic在2001年提出的方法，类似于I.Emery早先提出的方法[22]。

4. 绳结马赛克和镜像曲线

模块化在装饰艺术史上被非常有效和广泛地使用[18]。它是经济原则的一种体现，或者简单地说是如何使基本元素(模块)的数量最小化，同时使它们重组得到的不同装饰物(结构)的数量最大化的优化问题。模块化元素的一个典型示例是不同镶嵌的原型瓷砖，例如特鲁谢瓷砖，以及作为彭罗斯镶嵌基本元素的“风筝”和“飞镖”。一个不太为人所知的事实是，结镶嵌也是模块化的:规则正方形网格中的五种基本元素足以构建所有可能的结和链接的阴影。一位作者[23]提出了一组名为扭结拼块(图29)的这样的元素，R. Fathauer [24]也提出了一组类似的元素。第二组元素被S. Lomonaco和L. Kauffman用来构造结马赛克，并讨论它们与量子计算的联系[25]。T. Kyria证明了lomona-Kauffman猜想，即结马赛克相当于驯服结理论[26](图30和31)。在他的书《结:扭曲的数学》[27]中，索斯辛斯基注意到，交叉的平滑，有效地用于计算结多项式和获得结和链接的考夫曼状态的skein关系，只不过是在镜像曲线中放置双面镜子，凯尔特结大师用它来构建装饰他们的埋葬石、门赫什或手稿中的照明的结。在镜像曲线和结马赛克[28]中，我们展示了结马赛克、镜像曲线以及结和链接的网格(弧)表示的等价性。此外，我们还介绍了适用于计算机应用的镜像曲线代码，并用它们来计算结点和链节的考夫曼括号多项式和L多项式。

图29：S. Jablan的扭结拼块

图30：由8字结和波罗米亚环构成的绳结马赛克[25]

图31：[25]中的8字结和Borroean环被表示为镜像曲线[28]

图32：在手性向列相胶体[29]中合成的Borromean环632和缺失的链接622和92 49

镜像曲线的科学相关性最近在物理学论文《手性向列胶体中的可重构结和链节》[29]中得到证实(图32)。作者描述了一种使用激光镊子在向列相胶体中确定所谓土星环(胶体颗粒周围的单缺陷环)的方法。这种对土星环构型的控制使它们能够将所有向列型编织物归类为p × q胶体阵列，并将所有结和链节归类为4 × 4粒子阵列。以这种方式获得的结和链接代表了一类特殊的镜像曲线，只包含对应于粒子的正交叉。作者合成了几个例子，如霍普夫环、三叶形环和博洛门环，但随后设法区分了4 × 4中支持的几乎40种不同的结和链类型(省略了链622和92 49)。他们得出结论，拓扑对象的如此大的多样性表明，在足够大的胶体阵列上设计任何结或链接都是可能的。为了推广这些结果，我们从满足上述特定条件的p ≤ 6，q ≤ 6的维数为p × q的数组中生成所有的结和链。我们区分了1000多种不同的结和链接类型。然而，尽管我们知道镜像曲线等价于驯服结理论，即在足够大的网格中，所有的结和链接都可以实现为镜像曲线，但我们仍然无法证明所有的结和链接都可以实现为满足上述交叉和矩阵列的特定要求的镜像曲线。

5.现代雕塑和建筑中的结

虽然结通常被视为三维空间中的一维物体，但它们也可以在二维表面上看到。特别地，对于每个结，我们可以指定一种特殊的曲面，它的边界就是结本身，称为赛弗特曲面。从20世纪30年代开始，结、链接、源自它们的自回避曲线和赛弗特曲面在雕塑中得到了非常成功的应用，例如在纳姆·嘉宝、约翰·罗宾逊、查尔斯·佩里、卡洛·亮片和布伦特·科林斯的作品中(图33)。在当代艺术中，典型的例子是巴丝谢巴·格罗斯曼[30]的雕塑，由J.J .范·韦克[31]的“塞弗特观点”项目创作，或者是a .布拉托夫[32]的雕塑。

图33：查尔斯·o·佩里、约翰·罗宾逊和布伦特·柯林斯的雕塑

印度尼西亚编织和塔马利球启发了最初的张拉整体研究人员b .富勒和k .斯奈尔森在建筑中使用结和链接。在过去的几十年里，随着轻质材料、张拉整体和计算机设计工具的使用，他们的方法变得更加流行。最近的一些建筑项目，如北京的水立方，基于Waire-Phela结构，该结构为开尔文猜想提供了更好的解决方案，开尔文猜想是将空间最佳分割成等体积的单元，单元之间的表面积尽可能小(即什么是最有效的肥皂泡泡沫)，或斯图加特的UNStudio Mobius house和梅赛德斯-奔驰博物馆， 受莫比乌斯带的启发，将三叶形结解释为其Seifert表面的边界，开辟了思考其他世界的可能性，不同于数百年来主导建筑的笛卡尔网格、多面体或均匀间隔的网格系统[33]。这些项目是利用拓扑学、极小曲面、结、链接或非均匀空间镶嵌的思想发起的。

从数学的角度来看，代表结或链接的图是嵌入球体或平面的平面4价图，其额外的信息决定了线的过度和不足关系。在建筑学中，通过选择一个基本面，球体上的这种图可以很容易地转化为适合于建造柔性屋顶或冲天炉的半球形结构形式。在不同于球体的非平面表面上嵌入4价图是一个有趣的数学问题，在建筑方面有巨大的应用潜力。

5.1. 多面体结点和链接

由于多面体的规则性和对称性，几个世纪以来吸引了数学家、自然科学家和建筑师的注意。我们提出了几种结和链接的构造，这些结和链接来源于我们提出了几种结和链接的构造，这些结和链接来自于规则的、均匀的（阿基米德）和其他多面体。以这种方式获得的结和链接保留了原始多面体的重要对称性，代表了从纳米到宏观层面的多面体结结构的构建基础。

术语 "多面体链接 "代表了通过中边构造（图34a）或交叉曲线和双线覆盖（图34b）从不同的几何多面体得到的结和链接，以及交替源链接是指通过边的加倍而从3价几何多面体中衍生出来的（图34c）。

图34

1. 中线结构；(b)交叉曲线和双线覆盖构造；（c）边的加倍构造。断线表示在构建过程中删除的原图的边。

多面体图G的中间图M(G)是通过连接属于G的相邻边的G(图35a)的中间边点而得到的。得到的M(G)总是一个4价图，即一个基本多面体。另一方面，每一个至少3个顶点连通的基本多面体都是某种几何多面体的中间图。设DL是从M(G)通过交替地将4价顶点变成过交和欠交得到的一个连接图。请注意，初始图G是链接图DL的基础图，即G(DL) = G。因此，中间图的构造和通过忘记过欠信息将图变成图在某种意义上是相互逆的或对偶的。如果原始图G不包含有向图作为面，那么它的中间图也是如此。

图35. 来自Mathematica多面体数据库[34]的埃舍尔实体，以及通过中边构造从它和它的变换（截断的、星状的和几何化的埃舍尔实体）获得的基本多面体。

在论文[35,36]中提出了一种理解多面体链接构造的新方法。这些新方法涉及基于柏拉图和阿基米德实体的 "交叉曲线和双线覆盖 "构造（图36）。为了获得4价图，需要交叉曲线和边缘双线构造。交叉曲线构造包括用n条交叉曲线替换多面体图形的n个价位顶点，然后连接相邻的松散端，得到双线覆盖。

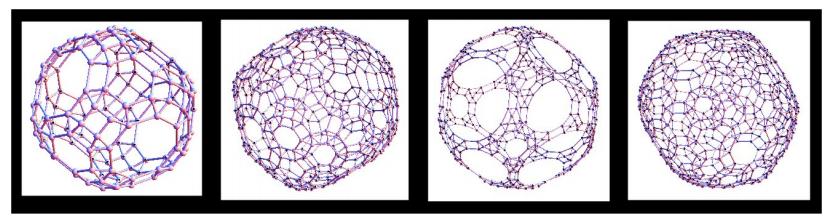
图36：从埃舍尔实体得到的基本多面体及其通过交叉曲线和双线覆盖的变换

从3-正则图中得到4-正则图，可以采用边倍构造法(图37b)：用双边(digon)[37]代替3个正则图的三条边中的一条。特别是，边加倍构造可以应用于截断多面体的富勒烯图，这些图总是3价的，产生各种多面体源链。

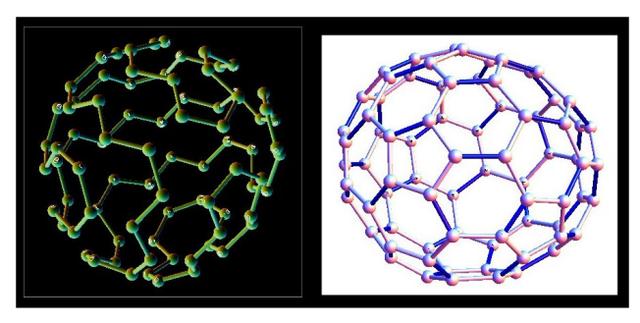
图37：富勒烯C60上的哈密顿循环和C60上的边加倍

随着数字技术的进步和超轻材料的出现，代表结和链接阴影的地面平面图现在变成了由柔性弹性杆制成的三维结构(图38)。未来的建筑不是刚体，而是可变形的实体，从平坦的4价网到它们的3D嵌入物，类似于D. Kozlov提出的NODUS结构[38]。常用的测地线圆顶大多基于刚性的3价图形，可以用4价柔性测地线圆顶或类似天然海绵结构的复杂结和链接来代替[39]。

图38：对应于纽结935和不同多面体纽结和链环的赛弗特曲面

6. 结论

结的发现可能早于火或车轮的发现。绳子、绳索和固定它们所需的结在早期技术发展中发挥了重要作用。没有发现这类文物的主要原因是，它们是由有机材料（植物纤维、筋腱、丁字裤、头发等）制成的，因此容易腐烂。早期使用绳索和绳结的间接证据是可追溯到大约30万年前的穿孔物体、珠子或吊坠，以及在非洲和中国发现的球形石头（大约50万年前），可能在打猎时用作博拉砝码。最近，需要精心制作的绳索和安全结的弓和箭，以及来自Kostenki（俄罗斯，公元前24,000年）的软石灰石中的旧石器时代雕像显示了由多个缠绕的柔性元件制成的腰带。在新西兰和丹麦保存的新石器时代的绳结很少。用枣树叶条编成的复杂的辫子源自古埃及。在秘鲁的quipus或新墨西哥州的Zuni结中，结的排列作为数学记录系统的基础，在那里结被用作象征和记忆的装置。在所有的古代文明中都可以找到各种绳结艺术的例子，在日本和中国的艺术、凯尔特人的艺术、泰米尔族和绍奎人的艺术、阿拉伯、希腊或斯密尔尼亚的花边中...... 在凯尔特艺术中，为装饰和宗教目的而创作的结绳图的广泛使用需要高水平的数学知识。精美的例子包括打结的曲线，甚至有放大的装饰物。在文艺复兴时期两位最杰出的艺术家和数学家的作品中，可以看到复杂的绳结构造。莱昂纳多·达芬奇和丢勒，以及米开朗基罗的绘画作品中都可以找到复杂的结构造。在现代艺术中，这种方法在纳姆-加波和其他建构主义雕塑家的创作中得到了体现。

我们几乎没有触及结在艺术中的众多应用，只详细讨论了少数几个，例如那些基于镜像曲线或多面体结构的结。其他一些结艺术的例子，如波斯马赛克（以及一般的马赛克中的结）、花边、纺织、马卡龙等，以及计算机艺术中的结，仍然不在本文的讨论范围之内。数学（结理论）、计算机科学和艺术相遇的一个最显著的例子是Rob Scharein的计算机软件KnotPlot[40]--它将是我们未来论文的一个主题，重点是结在艺术和科学中的作用。

参考文献

1. Przytycki, J.H. Knots: From combinatorics of knot diagrams to combinatorial topology based on knots. Available online: http://arxiv.org/pdf/math/0703096.pdf (accessed on 31 May 2012).

2. Bain, G. Celtic Art—The Methods of Construction; Dower: New York, NY, USA, 1973.

3. Allen, J.R. Celtic Art in Pagan and Cristian Times; Methuen and Co.: London, UK, 1904.

4. Gerdes, P. Sona Geometry from Angola: Mathematics of an African Tradition. Polimetrica International Science Publishers: Monza, Italy, 2006.

5. Gerdes, P. Geometry from Africa: Mathematical and Educational Explorations; The Mathematical Association of America: Washington, DC, USA, 1999.

6. Lissajous Knot. Available online: http://en.wikipedia.org/wiki/Lissajous knot (accessed on 31

May 2012).

7. Conway, J. An Enumeration of Knots and Links and Some of Their Related Properties. In Proceedings of the Conference Computational Problems, AbstractAlgebra, Oxford 1967; Leech, J., Ed.; Pergamon Press: New York, NY, USA, 1970.

8. Gerdes, P. Reconstruction and extension of lost symmetries. Comput. Math. Appl. 1989, 17, 791–813. (Also In Symmetry: Unifying Human Understanding II; Hargittai, I., Ed.; Pergamon Press: Oxford, UK, 1986).

9. Gerdes, P. On ethnomathematical research and symmetry. Symmetry Cult. Sci. 1990, 1, 154–170.

10. Gerdes, P. Une tradition geometrique en Afrique—Les dessins sur le sable, Volume 3: Analyse Comparative; L’Harmattan: Paris, France, 1995.

11. Gerdes, P. Ethnomathematik dargestellt am Beispiel der Sona Geometrie; Spektrum Verlag: Heidelberg, Germany, 1997.

12. Gerdes, P. Adventures in the World of Matrices; Nova Science Publishers (Series Contemporary Mathematical Studies): New York, NY, USA, 2008.

13. Gerdes, P. Lunda Geometry: Mirror Curves, Designs, Knots, Polyominoes, Patterns, Symmetries; Lulu: Morrisville, NC, USA, 2007.

14. Jablan, S.V. Mirror generated curves. Symmetry Cult. Sci. 1995, 6, 275–278. 15. Grunbaum, B.; Shephard, G.C. Tilings and Patterns; W.H.Freeman: New York, NY, USA, 1986.

16. Cromwell, P.R. Celtic knotwork: Mathematical art. Math. Intell. 1993, 15, 36–47.

17. Martin, G.E. Transformation Geometry. Springer-Verlag: New York, NY, USA, 1980.

18. Jablan, S.V. Symmetry, Ornament and Modularity, Series on Knots and Everything 30; World Scientifific: Singapore, 2002.

19. Shubnikov, A.V.; Koptsik, V.A. Symmetry in Science and Art; Plenum Press: New York, NY, USA, 1974.

20. Coxeter, H.S.M.; Moser, W.O.J. Generators and Relations for Discrete Groups; Springer-Verlag: New York, NY, USA, 1980.

21. Washburn, D.; Crowe, D.W. Symmetries of Culture; University of Washington Press: Seattle, DC, USA, 1988.

22. Emery, I. The Primary Structures of Fabrics. In Watson-Guptill Publications/Whitney Library of Design; The Textile Museum: Washington, DC, USA, 1995.

23. Crowe, D.W. Introduction to Slavik Jablan’s Modular Games. Available online: http://www.emis.de/journals/NNJ/Crowe.html (accessed on 31 May 2012).

24. Fathauer, R. KnoTiles. Available online:

http://mathartfun.com/shopsite sc/store/html/

Tessellations/MakingFaces.html (accessed on 31 May 2012).

25. Lomonaco, S.J.; Kauffman, L.H. Quantum knots and mosaics. Quantum Inf. Process. 2008, 7, 85–115.

26. Kuriya, T. On a lomonaco-kauffman conjecture. 2008. Avialable online:

http://arxiv.org/pdf/1106.3784.pdf (accessed on 31 May 2012).

27. Sossinsky, A. Knots—Mathematics with a Twist; Harvard University Press: Cambridge, MA, USA, 2002.

28. Jablan, S.; Radovic, L.J.; Sazdanovic, R.; Zekovic, A. Mirror-curves and knot mosaisc. Comput.Math. Appl. 2011, arXiv:1106.3784v2[math.GT].

29. Tkalec, U.; Ravnik, M.; Copar, S.; Zumer, S.; Musevic, I. Reconfifigurable knots and links in chiral nematic colloids. Science 2011, 333, 62–65, .

30. Grossman, B. Bathsheba Sculpture. Available online: http://www.bathsheba.com/ (accessed on 31 May 2012).

31. Van Wijk, J.J. Seifert View. Available online: http://www.win.tue.nl/∼vanwijk/seifertview/ (accessed on 31 May 2012).

32. Bulatov, A. Bulatov Abstract Creations. Available online: http://bulatov.org/ (accessed on 31 May 2012).

33. Vallisser, T. Other Geometries in Architecture: Bubbles, Knots and Minimal Surfaces. Available online:

http://www.springer.com/cda/content/document/cdadownloaddocument/978-88-470-1121-2 Wallisser.pdf (accessed on 31 May 2012).

34. Mathematica Polyhedron Data. Available online: http://reference.wolfram.com/mathematica/ref/

PolyhedronData.html/ (accessed on 31 May 2012).

35. Zhang, Y.; Seeman, N.C. Construction of a DNA-truncated octahedron. J. Am. Chem. Soc. 1994, 116, 1661–1669.

36. Qiu, W.-Y.; Zhai, X.-D. Molecular design of Goldberg polyhedral links.

J. Mol. Struc. (Theochem) 2005, 756, 163–166.

37. Jablan, S.; Sazdanovic. LinKnot—Knot Theory by Computer; World Scientifific: New Jersey, NJ, USA; London, UK; Singapore, 2007. Available online: http://math.ict.edu.rs/ (accessed on 31 May 2012); http://www.mi.sanu.ac.rs/vismath/linknot/index.html (accessed on 31 May 2012).

38. Kozlov, D. Topological Method of Construction of Point Surfaces as Physical Models. Available online: http://www.marhi.ru/AMIT/2008/spec08/papers/Kozlov/Kozlov02 paper EAEA2007.pdf (accessed on 31 May 2012) .

39. Burt, M. Periodical Sponge Structures and Uniform Sponge Polyhedra in Nature and in the Realm of the Theoretically Imaginable. Vismath 2007, 9, 4. Available online: http://www.mi.sanu.ac.rs/vismath/burt/index.html (accessed on 31 May 2012).

40. Scharein, R. KnotPlot. Available online: http://knotplot.com/ (accessed on 31 May 2012).

41. Slavik Jablan , Ljiljana Radovic , Radmila Sazdanovic and Ana Zekovic, Knots in Art

青山不改，绿水长流，在下告退。

转发随意，转载请联系张大少本尊。

,