python梯度上升法实现梯度下降（青少年Python编程）

对于一元二次函数的极值来说，可以通过配方法求得。但是，事实是我们生活的这个世界，绝大多数的函数都比一元二次函数要复杂，从而无法通过一些数学的公式化的手段来求得极值。

而现在，我们有了计算机，而计算机有极强的算力，我们就可以依托于计算机的算力以及一些算法来辅助我们对于原本无法求得极值的任意函数得到近似极值。

为什么是近似极值? 因为这是通过计算机的迭代计算得到的，而计算机是依托于浮点计算的，所以我们得到的是近似极值解。但是，这种近似解，已经够用了。试想，除了纯粹的数学，我们的世界哪里不是近似的？例如，时间，人们永远无法知道最精确的时间，因为人用来测量时间的工具是有误差的；同样，长度，重量。现实世界凡是人测出来的都是有误差的，只是误差可接受范围，这就是近似。

我们这里介绍的方法: 梯度下降方法求极值，也是人工智能领域，也就是机器学习最重要的方法，在机器学习领域，这个方法，也叫 反向传播，本质上就是梯度求极值，把参数学习到的过程。

我们依然先是以一元二次函数为例子，来介绍梯度下降法求极值。在下节课，会介绍对任意函数使用梯度下降求极值，并且介绍目前最主流的深度学习工具 pytorch.

我们仅仅以 a > 0, 有最小值的情况为例，函数是: , 配方法，我们可以知道，当 x=-1时，最小值是 y=1.

以计算机的思维考虑问题，计算机的能力是算力，可以快速的迭代。那么，如果我们应用这种能力到求解该一元二次函数的最小值。很自然的想到，我将定义域，这里假设是: [-1, 1], 我们将定义域分割成无数个点，也就形成了 , 接下来计算 , 我们将最小的 k 选取出来，就得到了最小值。显然, n取值越大，就越精细，那么，我们就能够得到越精确的值。

直接上代码。我们使用上节课，我们封装的一元二次函数类，来帮助我们计算函数的值。

importnumpyasnp importmatplotlib.pyplotasplt frommatplotlib.axesimportAxes fromprogramming.draw_curveimportdraw_line_by_kb fromprogramming.pointimportPoint fromprogramming.intervalimportInterval fromprogramming.quadratic_functionimportQuadraticFunction classMinValueByIterate: """ 迭代法求最小值 """ def__init__(self,n:int,interval:Interval): self.n=n self.interval=interval def__call__(self,qf:QuadraticFunction): points=qf.sample_points(interval=self.interval,num_points=self.n) y=[point.yforpointinpoints] x=[point.xforpointinpoints] index=np.argmin(y) returnPoint(x=x[index],y=y[index])

测试下，我们求得极值情况。在这里，我们对 n 的选择从 [2, 20]，选择不同的采样点来看看得到的极值情况。

qf=QuadraticFunction(a=1.0,b=2,c=2) items=list() forninrange(2,20): min_value=MinValueByIterate(n=n,interval=Interval(left=-2, right=2, is_left_closed=True, is_right_closed=True)) min_point=min_value(qf=qf) print(f"当x={min_point.x},最小值是{min_point.y}") items.append((n,min_point)) #绘制所有的最小值 min_value_draw_n=[item[0]foriteminitems] #使用直属换算，增加识别度 min_value_draw_y=[np.exp(item[1].y)foriteminitems] fig=plt.figure(num=1,figsize=(4,4))#创建画布 axes:Axes=fig.add_subplot(111)#创建坐标系 axes.grid()#设置坐标系样式 axes.set_aspect(1)#设置x,y坐标轴比例 axes.scatter(x=min_value_draw_n,y=min_value_draw_y,c="r") draw_line_by_kb(axes=axes,k=0,b=np.exp(1.0),begin_x=-1,end_x=25) plt.show()

当 x = -2.0, 最小值是 2.0 当 x = -2.0, 最小值是 2.0 当 x = -0.6666666666666667, 最小值是 1.1111111111111112 当 x = -1.0, 最小值是 1.0 当 x = -1.2, 最小值是 1.04 当 x = -1.3333333333333335, 最小值是 1.1111111111111112 当 x = -0.8571428571428572, 最小值是 1.0204081632653061 当 x = -1.0, 最小值是 1.0 当 x = -1.1111111111111112, 最小值是 1.0123456790123457 当 x = -1.2, 最小值是 1.04 当 x = -0.9090909090909092, 最小值是 1.0082644628099173 当 x = -1.0, 最小值是 1.0 当 x = -1.0769230769230769, 最小值是 1.0059171597633136 当 x = -1.1428571428571428, 最小值是 1.0204081632653061 当 x = -0.9333333333333333, 最小值是 1.0044444444444445 当 x = -1.0, 最小值是 1.0 当 x = -1.0588235294117647, 最小值是 1.0034602076124568 当 x = -1.1111111111111112, 最小值是 1.0123456790123457

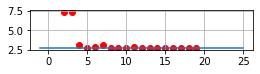
我们知道实际的最小值是 x=-1.0 时, y=1.0, 我们看到当我们的采样点只有很少的时候，2或3的时候，因为无法采样到 x=-1, 所以最小值是 2.0 与实际的 1.0 差距很大。当我们增大采样点的时候，越靠近 x=-1.0 的时候，得到的最小值越接近 y=1.0。

那是不是用这种方法就可以计算最小值了呢？理论上是可以的。但这里面还存在一些问题

1. 我们的采样区间如何确定？在这里我们直接将对称轴包含在了采样区间，而实际可能我们无法知道这种对称信息
2. 还有没有其他的极值点？这也是无法确定的。
3. 采样点设置多少个？间隔多少这也是一个问题。
4. 计算量与采样点一样，是不是能否缩减一些？

我们希望我们给定一个起始点，程序能够自动寻找最小值点的，这样就不用圈定采样区间了，当自动寻找到最小值的时候自动停止。这里我们介绍一个新的方法，梯度下降法来求解一元二次函数最小值。

我们观察一元二次函数的图像，我们发现对于图像上任意一个点，总是能够沿着一个方向向最小值前进，那么，这个变化的方向就是梯度，我们通过给梯度增加一个步长变化，使得 x 逐步的迭代就能够找到最小值。

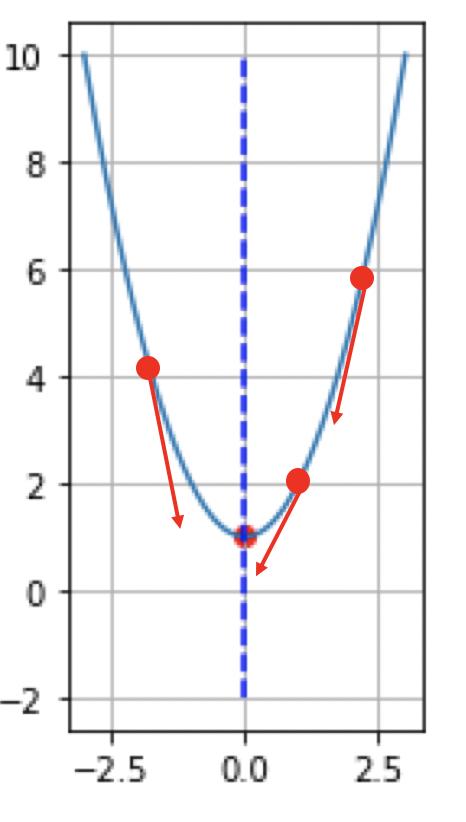
梯度就是在该点的导数。对于 来说，对 x 求导得到: , 迭代 .当 x = 1, , 我们沿着 -4 方向迭代; 当 x=-2时 , 我们沿着 2 方向迭代。

接下来我们就用梯度来对一元二次函数进行迭代，求解最小值吧。

我们针对 函数进行梯度计算，我们的类中有梯度计算成员函数，计算梯度的时候需要 学习率以及最大迭代步数。当我们找到一个比现在最小值大的就停止迭代。

classGradientDescent: """ 梯度下降 """ def_gradient(self,x:float): """ 梯度计算 """ return2*x 2 def__call__(self,int_x:float=None,learning_rate:float=0.01,num_steps:int=1000): x=int_x min_x=np.inf min_y=np.inf foriinrange(num_steps): x-=self._gradient(x)*learning_rate y=x*x 2*x 2 ify<min_y: min_x=x min_y=y else: break returni,Point(x=min_x,y=min_y)

测试下我们的梯度下降法求解的最小值吧.

gradient_descent=GradientDescent() step,point=gradient_descent(10,learning_rate=0.1,num_steps=1000) print(f"迭代了:{step}步,当{point.x}时，最小值是{point.y}")

迭代了: 90 步, 当 -0.9999999791314865 时，最小值是 1.0000000000000004

我们看到，当我们迭代了90步的时候，得到了最小值 1.0，x 与 -1.0 有一点误差，这并不要紧。

在这个过程中，我们并没有指定具体的区间，而是我们随机给了一个初始值 10（实际上可以给任何初始值），程序使用梯度下降自动寻找了最小值。是不是非常 Cool!

在这节课我们学习了如何使用计算机思维，并应用梯度下降法来求解最小值。这个方法与配方法比最大的优势在于，我们可以对任意函数进行最小值求解计算，而这就是人工智能最核心的算法-反向传播。

下节课，我们来看看如何对任意函数进行求解，并同时会介绍自动计算梯度的工具 pytorch，也是目前最主要的几个深度学习框架之一。