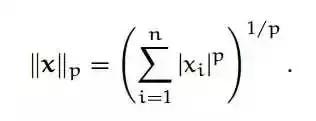系统线性代数（计算机科学中的线性代数）

选自arXiv

作者：Petros Drineas、Michael W. Mahoney

机器之心编译

参与：李泽南、刘晓坤、蒋思源

矩阵计算在计算机科学中占有举足轻重的地位，是每个开发者都需要掌握的数学知识。近日，来自普渡大学的 Petros Drineas 与 UC Berkeley 的 Michael Mahoney 提交了一篇概述论文《Lectures on Randomized Numerical Linear Algebra》可以作为线性代数知识的参考资料，本文将对其中的部分内容（主要为第二章：线性代数）进行简单介绍。

论文链接：arxiv.org/pdf/1712.08…

简介

矩阵在计算机科学、统计学和应用数学中占有独一无二的地位。一个 m×n 矩阵可以对 m 个对象（每个对象由 n 个特征描述）在有限单元网格中的离散微分算子信息进行描述；一个 n×n 正定矩阵可以编码所有 n 对象配对之间的相关性，或者网络中所有 n 节点对之间的边连通性等等。受科学和计算机技术发展的影响，近年来我们见证了矩阵算法理论和实践上令人兴奋的发展。其中最值得注意的是随机化的使用——通常假设由于生成机制的原因，输入数据存在噪声——它可以作为算法或计算资源用于开发和提升基础矩阵问题如矩阵乘法、最小二乘（LS）近似、低阶矩阵近似等算法。

如果 A 的所有列向量（或行向量）线性无关，那么 A 是可逆的。换句话说，不存在一个非零向量 x ∈ R^n 使得 Ax=0。可逆矩阵的标准性质有： (A^−1 )^⊤ = (A^⊤)^−1 = A^−⊤（A 逆的转置等于 A 转置的逆）和 (AB)^−1 = B^−1* A^−1（A 左乘 B 的逆等于 B 逆左乘 A 逆。注：微信表达式展示不便，准确表达式请查看原材料）。

正交矩阵：如果矩阵 A ∈ R^n×n 满足 A^⊤=A^−1，则称 A 为正交矩阵。等价地说，对所有 i , j 属于 [1,n]，正交矩阵满足：

对于 A 的行向量，上述性质同样满足。即 A 的所有列（或行）向量都是两两正交或互成法向量。

QR 分解：任意的矩阵 A ∈ R^n×n 都可以分解成一个正交矩阵和一个上三角矩阵的乘积：A=QR

其中 Q ∈ R^n×n 是正交矩阵，R ∈ R^n×n 是上三角矩阵。QR 分解在求解线性方程组的时候很有用，它的计算复杂度为 O(n^3)，并且是数值稳定的。为了用 QR 分解求解线性方程组 Ax=b，我们首先对等式两边同时左乘一个 Q^⊤，即 Q^⊤QRx = Rx = Q^⊤b。然后，我们用反向代入求解 Rx = Q^⊤b。

2.2 范数

范数（Norms）被用于度量矩阵的大小，或者相应地，度量向量的长度。范数是一个函数，它将 R^mxn（或 R^n）映射到 R。形式地说：

定义 1：任何函数满足 || · ||: R^m×n → R 和下列性质，则称为一个范数：

• 非负性：|| A ||≥0；|| A ||=0 当且仅当 A=0；
• 三角不等律：|| A B ||≤|| A || || B ||；
• 标量乘法律：|| αA ||=|α| || A ||，α∈R。

可以很容易地证明以下两个性质：

• || A ||=|| -A ||
• | || A ||-|| B || | ≤ || A-B ||

第二个性质被称为倒三角型不等式。

2.3 向量范数

若给定 n 维向量 x 和一个整数 p > 1，我们可以定义向量 p-范数为：

最常见的向量 p-范数为：

• 1-范数：

• 欧几里德（2）范数：

• 无穷（最大）范数：

若给定 n 维向量 x、y，我们可以使用 p-范数作为内积的上确界，即 Cauchy-Schwartz 不等式可以写为：

一般来说，该不等式给定了两个向量的欧几里德范数可以作为它们内积的上确界，Holder 不等式表明：

以下向量 p-范数的不等式性质可以轻易的证明：

2.4 归纳矩阵范数

给定一个 m×n 阶矩阵 A，和一个 p > 1 整数，我们定义矩阵的 p-范数为：

一般我们最常用的矩阵 p-范数为：

• 1-范数，取矩阵列加和绝对值的最大值：

• 无穷范数，取矩阵行加和绝对值的最大值：

• 2-范数，

这一系列的范数被称为「归纳（induced）」，因为它们是通过不取决于 A 和 p 的非零向量 x 而实现的。因此，一般存在一个单位范数向量（p-范数中的单位范数）x 令||A||p = ||Ax||p。归纳矩阵 p-范数遵循以下 submultiplicativity 法则：

此外，矩阵 p-范数对于矩阵的初等变换是不变的，即||PAQ||p = ||A||p，其中 P 和 Q 为对应维度的初等变换矩阵。同样，如果我们考虑矩阵分割：

那么子矩阵的范数就和全部矩阵的范数相关：即||B||p <= ||A||p。矩阵 p-范数间的以下关系可以相对简单地证明。若给定一个 m×n 阶矩阵，

此外，||A^T||1 = ||A||∞，||A^T||∞ = ||A||1。其中转置影响了矩阵的无穷范数和 1-范数，而不影响 2-范数，即||A^T||2 = ||A||2。同样，矩阵 2-范数并不会受到矩阵 pre(post)- multiplication 操作的影响，其中它的列（或行）为正交向量：||UAV^T||2 = ||A||2，其中 U 和 V 为对应维度的正交矩阵（U^T*U = I and V^T*V = I）。

2.6 奇异值分解

我们知道方阵可以分解为特征值与特征向量，但非方阵的矩阵并没不能实现特征值分解。因此奇异值分解（SVD）是每个矩阵中最重要的矩阵分解方式，因为不是所有的矩阵都能进行特征分解，但是所有的矩阵都能进行奇异值分解。

定义 6. 给定一个矩阵 A ∈ R^m×n，我们定义全 SVD 为：

其中 U ∈ R^m×m 和 V ∈ R^n×n 分别是包含 A 的左、右奇异向量的正交矩阵，Σ ∈ R^m×n 是对角矩阵，其中 A 的奇异值在主对角线上递减。

我们经常使用 u_i（或 v_j），i=1,..., m（或 j=1,..., n）来表示矩阵 U（或 V）的列。同样，我们将使用σ_i，i = 1,..., min{m, n} 来表示奇异值：

A 的奇异值是非负的，其数目等于 min{m, n}。A 的非零奇异值个数等于 A 的秩。由于正交不变性，我们得到：

其中 P 和 Q 是对应维度上的正交矩阵（P^TP = I 且 Q^TQ = I）。或者说，PAQ 的奇异值与 A 的奇异值相同。

涉及矩阵 A 和 B 的奇异值的以下不等式是非常重要的。首先，如果 A 和 B 都在 R^m×n 上，对于所有 i = 1, ... , min{m, n}，

第二，如果 A ∈ R^p×m 和 B ∈ R^m×n，对于所有 i = 1, ... , min{m, n}，

其中σ_1(A) = ||A||_2。我们经常对于仅保持非零奇异值和相应的（矩阵 A 的）左、右奇异向量感兴趣。给定矩阵 A ∈ R^m×n 和 rank(A)=ρ，我们可以定义它的稀疏 SVD。

定义 9. 给定矩阵 A ∈ R^m×n，秩为ρ ≤ min{m, n}，我们定义稀疏 SVD 为：

其中 U ∈ R^m×ρ和 V ∈ R^n×ρ是包含对应于非零奇异值的左、右奇异向量的两两正交列（即 U^TU = I 且 V^TV = I）的矩阵；Σ ∈ R^ρ×ρ是 A 的非零奇异值在对角线上递减的对角矩阵。

如果 A 是非奇异矩阵，我们可以使用 SVD 计算它的逆：

（如果 A 是非奇异的，那么它是方形和满秩的，在这种情况下，稀疏 SVD 和全 SVD 是一样的）众所周知，SVD 非常重要，任何矩阵的最佳 k 秩近似都可以通过 SVD 来计算。

定理 10. 让 A = UΣV^⊤ ∈ R^m×n 作为 A 的稀疏 SVD；设 k < rank(A) = ρ为整数，让

随后，

换句话说，上述定理指出，如果我们寻找一个矩阵 A 的 k 秩近似，使得「误差」矩阵的 2-范数或 Frobenius 范数最小化（即 A 和它的近似之间的差异最小化），随后我们需要保留 A 的最前 k 个奇异值和相应的左、右奇异向量。

我们会经常使用这些符号：让 U_k ∈ R^m×k（或 V_k ∈ R^n×k）表示矩阵 A 的最前 k 个左（或右）奇异向量的矩阵；让 Σ_k ∈ R^k×k 表示包含 A 的最前 k 个奇异值的对角矩阵。同样的，让 U_k,⊥ ∈ R^m×(ρ−k)（或 V_k,⊥ ∈ R^n×(ρ−k)）表示 A 的底部ρ-k 个非零左（或右）奇异向量的矩阵；然后令Σ_k,⊥ ∈ R^(ρ−k)×(ρ−k) 表示包含 A 的底部ρ-k 个奇异值的对角矩阵。然后，

2.9 Moore-Penrose 伪逆

对于非方矩阵而言，其逆矩阵是没有定义的。而一种非常出名的推广型矩阵求逆方法 Moore-Penrose 伪逆在这类问题上取得了一定的进展。形式上来说，若给定 m×n 阶矩阵 A，那么如果矩阵 A† 满足以下属性，它就是矩阵 A 的 Moore-Penrose 伪逆：

给定一个秩为ρ的 m×n 阶矩阵 A，它的稀疏奇异值分解可以表示为：

它的 Moore-Penrose 伪逆 A† 的稀疏奇异值分解可以表示为：

如果 A 为 n×n 阶满秩矩阵，那么 A† 就等于矩阵 A 的逆。如果 A 为 m×n 阶列满秩矩阵，那么 A†A 就等于 n 阶单位矩阵，AA†为矩阵 A 列上的投影矩阵。如果 A 为满行秩矩阵，那么 AA†就为 m 阶单位矩阵，A†A 为矩阵 A 行上的投影矩阵。

关于两个矩阵乘积的伪逆，有如下特别重要的属性：对于 m×p 阶矩阵 Y1 和 p×n 阶矩阵 Y2，且满足 Rank(Y1)=Rank(Y2)，即秩相等，[9, Theorem 2.2.3] 表明：

（我们强调秩相等的条件是非常重要的：因为两个矩阵相乘的逆总是等价于矩阵逆的相乘，但这个推断对于一般的 Moore-Penrose 伪逆 [9] 是不满足的）此外，Moore-Penrose 伪逆的基空间和所有实际的矩阵都有联系。给定一个矩阵 A 和 A 的 Moore-Penrose 伪逆 A†，A†的列空间可以定义为：

A†的列空间和零空间（null space）正交，A†的零空间可以定义为：

,