数学家费马简介（业余数学家之王）

17世纪是欧洲数学复兴的重要时期，以解析几何、微积分、概率论、射影几何为代表的新兴领域直接影响、决定了之后几个世纪的数学发展方向。在此期间，诞生了许多数学大家，其中最具代表性的有：牛顿、费马、笛卡尔、莱布尼茨、帕斯卡、惠更斯、卡瓦列里、沃利斯、笛沙格。

牛顿

这些数学家中，牛顿是是当之无愧的老大，有着微积分创始人身份（与莱布尼茨共享）的牛顿爵士，无论在应用数学还是纯数学上都有着17世纪数学家们难以企及的贡献。但是如果接着往下排序，牛顿之后你会选谁呢？

费马——是我的选择，相信你也不会反对，毕竟有着“业余数学王子”美誉的费马，对17世纪数学中最重要的三个领域——解析几何、微积分、概率论——都起到了决定性作用。费马与笛卡尔一起发明了解析几何，与帕斯卡、惠更斯共享了概率论的创立，他也是牛顿、莱布尼茨之前对微积分有着最大贡献的数学家。同时，费马还是继丢番图之后，欧拉、高斯之前对数论起主要推动的数学家。

费马（Pierre de Fermat，1601-1665）

解析几何

16世纪代数学有了很好的发展，三、四次方程的求根公式由塔尔塔利亚等意大利数学家陆续给出，“代数学之父”——韦达关于符号在代数上的使用更是让代数学飞速发展。到了17世纪，伽利略引入了“函数”的概念，用文字和比例的语言表达函数的关系。代数变得比以前重要了，但是几何自古希腊开始到17世纪初都还是数学家们研究数学的基础。

这一格局即将被打破，17世纪的两个重要发现：一个是解析几何、另一个是微积分，即将为代数的“王者之路”扫平障碍。

尺规作图问题历来被数学家们喜爱，17世纪的数学也不例外。生活在法国安德尔-卢瓦尔省的笛卡尔是一位著名的哲学家和数学家，他因为一句“我思故我在”名扬中外。1637年，笛卡尔发表了论文《几何》，该册子第一部分并不特别，笛卡尔继续韦达的研究，把几何作图问题转化为代数运算问题；但是当读者阅读到第二部分时，彻底的“懵”了，笛卡尔作出了一个惊人的举动：使用代数方程去研究曲线，他将研究的曲线用两段距离表示，这样会得到一个二元方程。没错，这就是“解析几何”第一次给人们见面。

正当笛卡尔为自己的研究而倍感自豪时，“业余数学家”费马有想法了。《平面和立体的轨迹引论》(1679)是费马1629年完成的著作，但直到他去世14后才发表，此书比笛卡尔更早的提出了“解析几何”的思想。

笛卡尔

费马的工作是从研究古希腊数学家的著作开始的。首先，他重新写出了古希腊数学家阿波罗尼奥斯的几何学著作《论平面轨迹》。接着，他从丢番图出发研究了算术，并受韦达代数研究的影响。在他看来，古人对于几何问题的研究技巧性太强，几乎一题一解、不具一般性；同时，当时的代数研究缺乏基础，与几何的严谨性形成鲜明的对比，但是对于思维量的要求则要小得多。一个天才的想法产生了：为何不把代数和几何结合起来，取长补短，而更好的服务于数学研究呢？

费马的做法是这样的：如图，曲线上任意一点J的位置由两个线段OZ和ZJ决定，记他们的长度分别为A和E。这样根据一定的运算，可以得到这条曲线所对应的二元方程。费马意识到不同坐标系会得到不同复杂程度的方程，但是如果A和E都是1次时，该曲线为直线。当A或E为2次时，该曲线代表圆锥曲线。

从今天的角度来看，费马的坐标轴只有x轴（图中OZ）,而没有y轴，这里的A、Z分别相当于横坐标x和纵坐标y。费马的坐标系也非我们现在常用的直角坐标系，而是比较复杂的斜坐标系(一个例外是在费马推导切线时，他用到了直角坐标系，见下文)。同时，根据费马的坐标系，得到的点的坐标也只有“正数和0”而没有负数。

这些“瑕疵”在一个发明的初期是值得原谅的，毕竟他们只是开路人，后期完善和美化还需后人来完成。不管是费马还是笛卡尔，在探索“解析几何”的路上他们做出了最伟大的贡献，他们将两个看似不相容的领域融合到了一起。从此，人们可以利用代数知识来证明关于曲线（几何）的任何性质，摆脱了几何学复杂的“脑力活动”，而归于自动化的计算。同时，将方程（代数）转化为几何对象，赋予其几何意义，可以更直观的研究代数对象。还有一点更为重要的是，“解析几何”的发现为17世纪最伟大的发明——微积分铺平了道路。

微积分

文艺复兴后的17世纪，数学家们致力于解决4类科学问题，并最终导致了微积分的发明。

（1）已知物体运动距离s关于时间t的函数，求瞬时速度v或加速度a.

（2）求曲线的切线.

（3）求函数的最大值和最小值.

（4）求曲线长度、曲面面积.

问题（1）实质是物理中关于变化率的问题，一般解法要直到牛顿才给出。问题（2）-（4）在牛顿之前已由费马、Wallis 等数学家给出个例解答，并最终由牛顿、莱布尼茨进行高度统一为函数求积和求导的过程。牛顿已经认识到函数求积、求导的互逆性，并使用“广义二项式定理”将超越函数（如y=sinx等）展开为多项式的形式、再进行求微积分。

牛顿的关于微积分的创造性工作让他在纯数学领域得到了足够大的名声。但他自己也坦言：“如果说我看得比别人更远些，那是因为我站在巨人的肩膀上”。根据牛顿的记录，这些巨人中就包括费马。

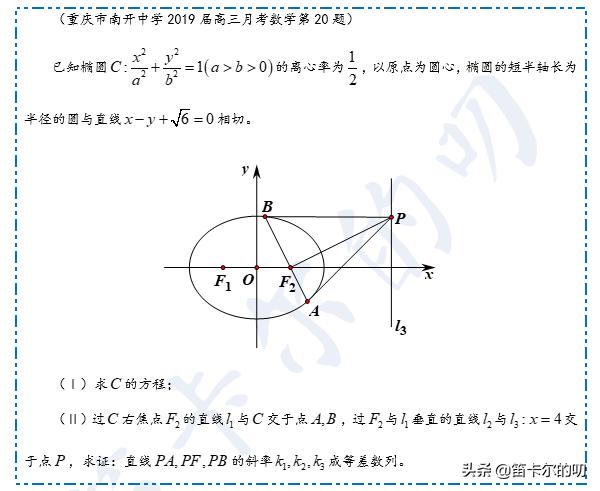
费马关于微积分的先见性工作主要集中在处理问题（2）-（4）上。对于问题（2）,费马（也包括笛卡尔）首次将切线定义为“割线的极限”（17世纪以前由于曲线都是指通过尺规作出的图形，切线一般是指与曲线只有一个交点的直线）.因此，费马求切线的过程，相当于是割线的逼近过程。具体如下：

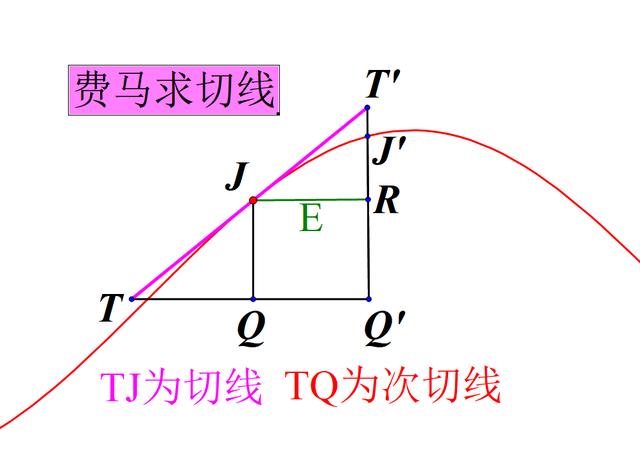
如图，以T为坐标原点，则TQ为横坐标x,QJ为纵坐标f(x).当E很小时，根据△TJQ∽△JRT’，且T’R≈J’R.于是TQ:JQ=E:(J’Q’-RQ’).即， x:f(x)=E:(f(x E)-f(x)). 最后，令E=0,就可计算出TQ(或x)的值，进一步切线TJ也就确定了。这样的解法与我们现在求切线的方法一致，E为增量△x.改写为今天的形式

（△x→0）相当于切线的斜率。费马的先见之明着实让我们震撼。

接下来是问题（3），费马的思想如下：设自变量x增加到x △x,当函数y=f(x)在极值处时，函数f(x)与f(x △x)是相等的。这样得到的两个方程联立，再使得△x=0.就可解得极值。

从现在角度来看，费马其实已经意识到了极值点处函数的导函数等于0（所以才有f(x)与f(x △x)是相等）。最后是问题（4），1936年，费马用现在我们所用的方式求出了函数

曲线下的面积，用现在的符号表示为：

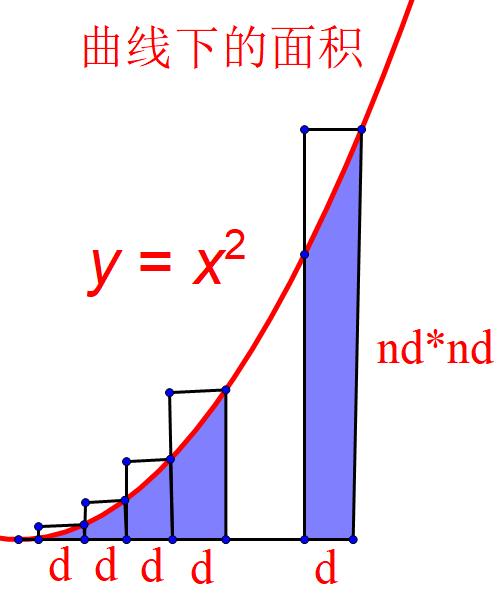
尽管n=-1，即y=1/x的积分费马并没有给出，但是1647年，圣文森特在他的著作《几何著作》中，使用费马的方法得到了其结果为klogy.

从上面的分析我们知道，费马为微积分的成型其实已经做了大量的独创性工作，求切线、求面积的方法为微积分提供了一般性解决方案。而且在一定程度上，牛顿、莱布尼茨的工作就是建立在费马和其他数学家工作的基础上的，但是费马并没有对它们进行高度有效的统一，他也没有“广义二项式定理”这样有效的工具——可以将超越函数转化为多项式来求积或求导。

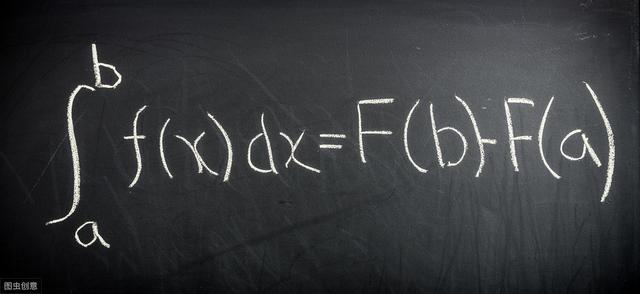
但是作为一个“业余数学家”来说，这样的工作已经是无人能及了。接下来再看看费马的另一项重要贡献——概率论。

概率论

概率论起源于赌博，包括16世纪著名数学家卡尔达诺（Cardano）就已研究过掷骰子中遇到的一些简单问题，但是概率真正起源要归功于三个人：帕斯卡、费马和惠更斯。

17世纪，法国赌徒梅内（Méré）就一个赌资分配问题请教帕斯卡（ Pascal，1623-1662），于是有了帕斯卡和费马关于“点数分配问题”的著名讨论。

经过简化，我们可以这样简化梅内遇到的问题：甲、乙两人抛硬币，甲赌“正(Z)”，乙赌“反(F)”，赢家每次得1分，并各下赌注10元，先得10分者获取所有赌注。但是赌博在“甲8分、乙7分”时中断，问应该如何分配这20元赌注？

费马发现这样的赌局至多需要4局就可以判断甲、乙的输赢，因此他列举了所有的情况，并根据“期望值”来分赌注。

经过统计，在这16种结果中，有11种情况是“甲赢”，而另外5种是“乙赢”。因此甲可分得20×11/16，而乙可分得20×5/16.这与帕斯卡的方法殊途同归。

最后，“期望值”的概念也被同时代荷兰著名数学家惠更斯( Huygens，1629-1695年)写进他的《论赌博中的计算》（1657）一书中，这是真正意义上的第一部概率论著作。但是数学家们仍然喜欢把1654年7月29日定为概率论的“生日”，因为这天是费马与帕斯卡就“梅内问题”通信的日子。

自惠更斯以后，再经伯努利、拉普拉斯、柯尔莫哥洛夫等数学家的努力，概率论成为了当今社会不可或缺的数学理论。

数论

解析几何、微积分、还有数论，让这位“业余数学王子”进入了顶级数学家行列，但是我想最让费马爱不释手的，还是数论。他从古希腊数学家丢番图哪里开始学习数论。

费马研习丢番图的《算术》，并将书中不定方程的研究限制在整数范围内，从而开始了数论这门数学分支。关于《算术》的笔注让他有了“吹牛皮”的嫌疑，比如费马大定理：

n>2是整数，则方程x^n y^n=z^n没有满足xyz≠0的整数解.

在书页旁边，费马备注到：“将一个立方数分成两个立方数之和，或一个四次幂分成两个四次幂之和，或者一般地将一个高于二次的幂分成两个同次幂之和，这是不可能的。关于此，我确信已发现了一种美妙的证法 ，可惜这里空白的地方太小，写不下”

费马轻描淡写一句话，让数学家们忙活了几百年，而直到1995年，才由英国数学家怀尔斯予以证明。

当然，费马不止有“费马大定理”，列举其他主要成果如下：

○费马小定理：a^p-a≡0(mod p)，其中p是一个素数，a是正整数

○全部大于2的素数可分为4n 1和4n 3两种形式。

○形如4n 1的素数能够，而且只能够以一种方式表为两个平方数之和。

○没有一个形如4n 3的素数，能表示为两个平方数之和。

○4n 1形的素数与它的平方都只能以一种方式表达为两个平方数之和

......

生活

费马生来富贵，一生无忧。他的父亲是一位商人，母亲为贵族。尽管费马可以全凭实力打拼，但生活在“卖官卖爵”(法国)泛滥的17世纪，费马大学还没有毕业，家里就给他在洛马涅买好了“律师”和“参议员”的职位。这一入行就是一辈子，他这一生都是一个全职的律师。但也正是因为律师的职业，让他有了比其他人更多的时间来研究数学，并取得了骄人的成就。

参考文献：

1.克莱因.古今数学思想.上海科学技术出版社.2009

2.梁宗巨.世界数学通史（上）.辽宁教育出版社.2005

,